题目内容
 如图,AE是⊙O的直径,弦AB=BC=4
如图,AE是⊙O的直径,弦AB=BC=4| 2 |
考点:扇形面积的计算
专题:
分析:根据弦AB=BC,弦CD=DE,可得∠BOD=90°,∠BOD=90°,过点O作OF⊥BC于点F,OG⊥CD于点G,在四边形OFCG中可得∠FCD=135°,过点C作CN∥OF,交OG于点N,判断△CNG、△OMN为等腰直角三角形,分别求出NG、ON,继而得出OG,在Rt△OGD中求出OD,即得圆O的半径,代入扇形面积公式求解即可.
解答: 解:∵AB=BC,CD=DE,
解:∵AB=BC,CD=DE,
∴点B是弧AC的中点,点D是弧CE的中点,
∴∠BOD=90°,
过点O作OF⊥BC于点F,OG⊥CD于点G.则BF=FC=2
,CG=GD=2,∠FOG=45°,
在四边形OFCG中,∠FCD=135°,
过点C作CN∥OF,交OG于点N,
则∠FCN=90°,∠NCG=135°-90°=45°,
∴△CNG为等腰三角形,
∴CG=NG=2,
过点N作NM⊥OF于点M,则MN=FC=2
,
在等腰三角形MNO中,NO=
MN=4,
∴OG=ON+NG=6,
在Rt△OGD中,OD=
=
=2
,
即圆O的半径为2
,
故S阴影=S扇形OBD=
=10π.
故答案为:10π.
 解:∵AB=BC,CD=DE,
解:∵AB=BC,CD=DE,∴点B是弧AC的中点,点D是弧CE的中点,
∴∠BOD=90°,
过点O作OF⊥BC于点F,OG⊥CD于点G.则BF=FC=2
| 2 |
在四边形OFCG中,∠FCD=135°,
过点C作CN∥OF,交OG于点N,
则∠FCN=90°,∠NCG=135°-90°=45°,
∴△CNG为等腰三角形,
∴CG=NG=2,
过点N作NM⊥OF于点M,则MN=FC=2
| 2 |
在等腰三角形MNO中,NO=
| 2 |
∴OG=ON+NG=6,
在Rt△OGD中,OD=
| OG2+GD2 |
| 62+22 |
| 10 |
即圆O的半径为2
| 10 |
故S阴影=S扇形OBD=
90π×(2
| ||
| 360 |
故答案为:10π.
点评:本题考查了扇形的面积计算、勾股定理、垂径定理及圆心角、弧之间的关系,综合考查的知识点较多,解答本题的关键是求出⊙0的半径,此题难度较大.

练习册系列答案
相关题目
 如图是一个包装纸盒的三视图(单位cm),则制作一个纸盒所需纸板的面积是多少?
如图是一个包装纸盒的三视图(单位cm),则制作一个纸盒所需纸板的面积是多少? 如图,OP平分∠AOB,点C在OA上,OC=4,△OPC的面积为6,求点P到OB的距离.
如图,OP平分∠AOB,点C在OA上,OC=4,△OPC的面积为6,求点P到OB的距离. 如图是一块从一个边长为50cm的正方形材料中裁出的垫片,现测量FG=8cm,求这个垫片的周长.
如图是一块从一个边长为50cm的正方形材料中裁出的垫片,现测量FG=8cm,求这个垫片的周长. 已知⊙O的外切等腰梯形ABCD的腰长为10,⊙O的半径为3,求等腰梯形ABCD的面积及下底的长.
已知⊙O的外切等腰梯形ABCD的腰长为10,⊙O的半径为3,求等腰梯形ABCD的面积及下底的长. 如图,六边形ABCDEF的内角都相等,∠BAD=60°,AB与ED、AD与FE有怎样的位置关系?为什么?
如图,六边形ABCDEF的内角都相等,∠BAD=60°,AB与ED、AD与FE有怎样的位置关系?为什么?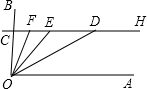 如图,在∠AOB的边OB上取一点C,过点C作CH∥OA,D、E、F在CH上,且满足OD平分∠EOA,OF平分∠COE,∠AOB=88°.
如图,在∠AOB的边OB上取一点C,过点C作CH∥OA,D、E、F在CH上,且满足OD平分∠EOA,OF平分∠COE,∠AOB=88°.