题目内容
若2a+b=10,其中a≥0,b≥0,又P=5a+2b.求P的取值范围.
考点:解二元一次方程组,解一元一次不等式组
专题:
分析:先求出a的取值范围,把P中的b消去列出含a的式子,再求出P的取值范围.
解答:解:∵2a+b=10
∴b=10-2a
∵b≥0,
∴10-2a≥0,
解得a≤5
∵a≥0,
∴0≤a≤5
∵P=5a+2b
∴P=5a+2(10-2a)=20+a
∴20≤P≤25.
∴b=10-2a
∵b≥0,
∴10-2a≥0,
解得a≤5
∵a≥0,
∴0≤a≤5
∵P=5a+2b
∴P=5a+2(10-2a)=20+a
∴20≤P≤25.
点评:此题考查了解二元一次方程组,一元一次不等式组.解题的关键是求出a的取值范围再求P的取值范围.

练习册系列答案
相关题目
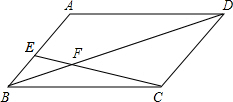 如图,在?ABCD中,E在AB上,CE、BD交于F,若AE:BE=4:3,且BF=2,则DF的长为( )
如图,在?ABCD中,E在AB上,CE、BD交于F,若AE:BE=4:3,且BF=2,则DF的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
菱形ABCD的对角线AC=5,BD=10,则该菱形的面积为( )
| A、50 | ||||
| B、25 | ||||
C、
| ||||
| D、12.5 |
 如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,在第
如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,在第 如图,∠A,∠D为直角,AC与DB相交于点E,BE与EC相等,在图中找出两对全等三角形并说明理由.
如图,∠A,∠D为直角,AC与DB相交于点E,BE与EC相等,在图中找出两对全等三角形并说明理由. 已知,如图,O是△ABC高AD与BE的交点,∠C=50°,求∠AOB的度数.
已知,如图,O是△ABC高AD与BE的交点,∠C=50°,求∠AOB的度数. 已知如图,EF、AD被AB、BC所截,且EF∥AD,∠1=∠2.求证:AB∥DH.
已知如图,EF、AD被AB、BC所截,且EF∥AD,∠1=∠2.求证:AB∥DH.