Question

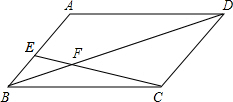如图，在?ABCD中，E在AB上，CE、BD交于F，若AE：BE=4：3，且BF=2，则DF的长为（　　）

• A、

  5

  3

• B、

  7

  3

• C、

  10

  3

• D、

  14

  3

Answer 1

考点：平行四边形的性质,相似三角形的判定与性质

专题：

分析：利用平行四边形的性质得出△EBF∽△CDF，再利用相似三角形的性质得出DF的长．

解答：解：∵在?ABCD中，
∴BE∥CD，AB=CD，
∴△EBF∽△CDF，
∴

BF

DF

=

BE

CD

，
∵AE：BE=4：3，且BF=2，
∴

BF

DF

=

BE

CD

=

3

7

=

2

DF

，
∴DF=

14

3

．
故选：D．

点评：此题主要考查了平行四边形的性质以及相似三角形的性质与判定，得出△EBF∽△CDF是解题关键．