题目内容
 如图,∠A,∠D为直角,AC与DB相交于点E,BE与EC相等,在图中找出两对全等三角形并说明理由.
如图,∠A,∠D为直角,AC与DB相交于点E,BE与EC相等,在图中找出两对全等三角形并说明理由.考点:全等三角形的判定
专题:
分析:根据∠A=∠D,∠AEB=∠DEC,BE=EC得出△ABE≌△DCE;利用上面的结论得出AB=DC,进一步利用“HL”得出△ABC≌△DCB.
解答:解:①△ABE≌△DCE.
理由:在△ABE和△DCE中,
,
∴△ABE≌△DCE(AAS);
②△ABC≌△DCB.
理由:∵△ABE≌△DCE
∴AB=DC,
在Rt△ABC和Rt△DCB中,
,
∴Rt△ABC≌Rt△DCB(HL).
理由:在△ABE和△DCE中,
|
∴△ABE≌△DCE(AAS);
②△ABC≌△DCB.
理由:∵△ABE≌△DCE
∴AB=DC,
在Rt△ABC和Rt△DCB中,
|
∴Rt△ABC≌Rt△DCB(HL).
点评:此题考查三角形全等的判定,结合图形,掌握判定的方法是解决问题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
下列等式从左到右的变形中,属于因式分解的是( )
| A、x2-6x+9=(x-3)2 |
| B、(x+3)(x-1)=x2+2x-3 |
| C、x2-9+6x=(x+3)(x-3)+6x |
| D、6ab=2a•3b |
先作二次函数y=2x2+bx+c关于x轴对称的图象,再绕图象的顶点旋转180度,得到二次函数y=ax2-8x+5,则a、b、c的取值分别是( )
| A、2,-8,11 |
| B、2,-8,5 |
| C、-2,-8,11 |
| D、-2,-8,5 |
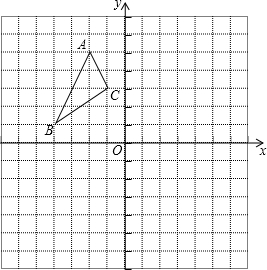 利用图中的网格线(最小的正方形的边长为1)画图:
利用图中的网格线(最小的正方形的边长为1)画图: