题目内容
在△ABC和△A′B′C′中，已知AB=6，BC=8，AC=10，A′B′=18，B′C′=24，A′B′=30，求证：△ABC∽△A′B′C′．
考点：相似三角形的判定
专题：
分析：利用“三边法”来证明：△ABC∽△A′B′C′．
解答：证明：∵在△ABC和△A′B′C′中，已知AB=6，BC=8，AC=10，A′B′=18，B′C′=24，A′B′=30，
∴
=
=
，
=
=
，
=
=
=
=
，
∴△ABC∽△A′B′C′．
∴
| AB |
| A′B′ |
| 6 |
| 18 |
| 1 |
| 3 |
| BC |
| B′C′ |
| 8 |
| 24 |
| 1 |
| 3 |
| AC |
| A′C′ |
| 10 |
| 30 |
| 1 |
| 3 |
| AB |
| A′B′ |
| BC |
| B′C′ |
| AC |
| A′C′ |
∴△ABC∽△A′B′C′．
点评：本题考查了相似三角形的判定．三边法：三组对应边的比相等的两个三角形相似．
练习册系列答案
相关题目
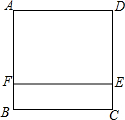如图，从正方形ABCD上截取宽为2cm的矩形BCEF，剩下矩形AFED的面积为48cm2，则正方形ABCD的边长为
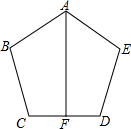如图，AB=AE，BC=ED，∠B=∠E，求证：∠BCD=∠EDC．