题目内容
半径为1的⊙O中,两条弦AB=
,AC=1,∠BAC的度数为 .
| 2 |
考点:垂径定理,解直角三角形
专题:分类讨论
分析:分类讨论:当AC与AB在点A的两旁.由OA=OC=1,AC=1,得到△OAC为等边三角形,则∠OAC=60°,又由OA=OB=1,AB=
,得到△OAB为等腰直角三角形,则∠OAB=45°,所以∠BAC=45°+60°=105°;当AC与AB在点A的同旁.有∠BAC=∠OAC-∠OAB=60°-45°=15°.
| 2 |
解答: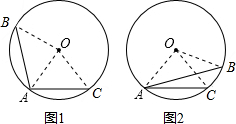 解:如图1,当AC与AB在点A的两旁.
解:如图1,当AC与AB在点A的两旁.
连OC,OA,OB,如图,
在△OAC中,
∵OA=OC=1,AC=1,
∴△OAC为等边三角形,
∴∠OAC=60°;
在△OAB中,
∵OA=OB=1,AB=
,即12+12=(
)2,
∴OA2+OB2=AB2,
∴△OAB为等腰直角三角形,
∴∠OAB=45°,
∴∠BAC=45°+60°=105°;
如图2,当AC与AB在点A的同旁.
同(1)一样,可求得∠OAC=60°,∠OAB=45°,
∴∠BAC=∠OAC-∠OAB=60°-45°=15°.
综上所述:∠BAC的度数为:105°或15°.
故答案为:105°或15°.
 解:如图1,当AC与AB在点A的两旁.
解:如图1,当AC与AB在点A的两旁.连OC,OA,OB,如图,
在△OAC中,
∵OA=OC=1,AC=1,
∴△OAC为等边三角形,
∴∠OAC=60°;
在△OAB中,
∵OA=OB=1,AB=
| 2 |
| 2 |
∴OA2+OB2=AB2,
∴△OAB为等腰直角三角形,
∴∠OAB=45°,
∴∠BAC=45°+60°=105°;
如图2,当AC与AB在点A的同旁.
同(1)一样,可求得∠OAC=60°,∠OAB=45°,
∴∠BAC=∠OAC-∠OAB=60°-45°=15°.
综上所述:∠BAC的度数为:105°或15°.
故答案为:105°或15°.
点评:本题考查了圆周角定理.在同圆或等圆中,同弧和等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.同时考查了特殊三角形的边角关系和分类讨论的思想的运用.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 如图所示的图形旋转一定角度后能与自身重合,则旋转的角度可以是( )
如图所示的图形旋转一定角度后能与自身重合,则旋转的角度可以是( )| A、30° | B、45° |
| C、60° | D、90° |
 在△ABC中,若BC>BA,AD、CE是两条高,求证:BC+AD>AB+CE.
在△ABC中,若BC>BA,AD、CE是两条高,求证:BC+AD>AB+CE. 已知:如图,平行四边形ABCD中,∠ADC的平分线与AB相交于点E.求证:BE+BC=CD.
已知:如图,平行四边形ABCD中,∠ADC的平分线与AB相交于点E.求证:BE+BC=CD. 已知:实数a,b在数轴上的位置如图所示,化简:
已知:实数a,b在数轴上的位置如图所示,化简: