题目内容
10.先化简,再求值$\frac{1}{x(x-1)}+\frac{1}{(x-1)(x-2)}+\frac{1}{(x-2)(x-3)}$,其中x=2.分析 首先对分式进行通分,然后进行分式的加法计算,然后对结果进行约分,然后代入数值计算即可.
解答 解:原式=$\frac{(x-2)(x-3)+x(x-3)+x(x-1)}{x(x-1)(x-2)(x-3)}$
=$\frac{{x}^{2}-5x+6+{x}^{2}-3x+{x}^{2}-x}{x(x-1)(x-2)(x-3)}$
=$\frac{3{x}^{2}-9x+6}{x(x-1)(x-2)(x-3)}$
=$\frac{3(x-1)(x-2)}{x(x-1)(x-2)(x-3)}$
=$\frac{3}{x(x-3)}$.
当x=2时,原式=$\frac{3}{2×(2-3)}$=-$\frac{3}{2}$.
点评 本题考查了分式的化简求值,解这类题的关键是利用分解因式的方法化简分式.

练习册系列答案
相关题目
1.小颖、小丽、小虎三位同学的身高如下表所示.
(1)以小丽身高为标准,记作0cm,用有理数表示出小颖和小虎的身高.
(2)若小颖身高记作-8cm,那么小虎和小丽的身高应记作多少cm..
| 姓名 | 小虎 | 小颖 | 小丽 |
| 身高(cm) | 155 | 150 | 147 |
(2)若小颖身高记作-8cm,那么小虎和小丽的身高应记作多少cm..
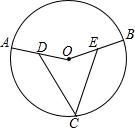 如图,在⊙O中,点C是优弧ACB的中点,D、E分别是OA、OB的中点,求证:CD=CE.
如图,在⊙O中,点C是优弧ACB的中点,D、E分别是OA、OB的中点,求证:CD=CE.