题目内容
5.已知a=1990x+1989,b=1990x+1990,c=1990x+1991,求a2+b2+c2-ab-ac-bc的值.分析 已知条件中的几个式子有中间变量x,三个式子消去x即可得到:a-b=-1,c-a=2,b-c=-1,用这三个式子表示出已知的式子,即可求值.
解答 解:∵a=1990x+1989,b=1990x+1990,c=1990x+1991,
∴a-b=-1,b-c=-1,c-a=2.
∴a2+b2+c2-ab-ac-be
=$\frac{1}{2}$(2a2+2b2+2c2-2ab-2bc-2ac)
=$\frac{1}{2}$[(a2-2ab+b2)+(b2-2bc+c2)+(c2-2ac+a2)]
=$\frac{1}{2}$[(a-b2)+(b-c)2+(c-a)2]
=$\frac{1}{2}$[(-1)2+(-1)2+22]
=$\frac{1}{2}$(1+1+4)
=3.
点评 此题主要考查了因式分解的应用,根据题意正确的利用完全平方公式分解因式是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.下列命题中假命题的是( )
| A. | 同位角相等 | |
| B. | 同旁内角互补,两直线平行 | |
| C. | 等角的余角相等 | |
| D. | 过一点能且只能作一条直线和直线平行 |
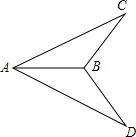 如图,已知AC=AD,∠CAB=∠DAB,求证:∠C=∠D.
如图,已知AC=AD,∠CAB=∠DAB,求证:∠C=∠D. 如图所示的阴影部分面积用代数式表示为ab-$\frac{1}{2}π{b}^{2}$.
如图所示的阴影部分面积用代数式表示为ab-$\frac{1}{2}π{b}^{2}$. 已知一次函数y=kx+b的图象与x轴交于点A,与y轴交于点B(0,2),且与正比例函数y=$\frac{4}{3}$x的图象交于点C(m,4)
已知一次函数y=kx+b的图象与x轴交于点A,与y轴交于点B(0,2),且与正比例函数y=$\frac{4}{3}$x的图象交于点C(m,4) 如图,∠B=∠E=90°,AB=a,DE=b,AC=CD,∠D=60°,∠A=30°,则BE=a+b.
如图,∠B=∠E=90°,AB=a,DE=b,AC=CD,∠D=60°,∠A=30°,则BE=a+b.