题目内容
2.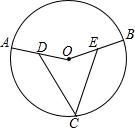 如图,在⊙O中,点C是优弧ACB的中点,D、E分别是OA、OB的中点,求证:CD=CE.
如图,在⊙O中,点C是优弧ACB的中点,D、E分别是OA、OB的中点,求证:CD=CE.
分析 首先连接OC,由在⊙O中,点C是优弧ACB的中点,根据圆心角与弧的关系,可得∠COD=∠COE,又由D、E分别是OA、OB的中点,可得OD=OE,然后由SAS判定△COD≌△COE,继而证得结论.
解答 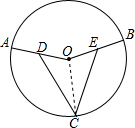 证明:连接OC,
证明:连接OC,
∵在⊙O中,点C是优弧ACB的中点,
∴∠AOC=∠BOC,
∵D、E分别是OA、OB的中点,OA=OB,
∴OD=OE,
在△COD和△COE中,
$\left\{\begin{array}{l}{OC=OC}\\{∠COD=∠COE}\\{OD=OE}\end{array}\right.$,
∴△COD≌△COE(SAS),
∴CD=CE.
点评 此题考查了圆心角与弧的关系以及全等三角形的判定与性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
11.在Rt△ABC中,∠C=90°,AB=2BC,那么sinA的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
12.在实数0,π,$\frac{12}{11}$,-$\sqrt{4}$,$\sqrt{3}$中,是无理数的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
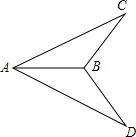 如图,已知AC=AD,∠CAB=∠DAB,求证:∠C=∠D.
如图,已知AC=AD,∠CAB=∠DAB,求证:∠C=∠D. 如图所示的阴影部分面积用代数式表示为ab-$\frac{1}{2}π{b}^{2}$.
如图所示的阴影部分面积用代数式表示为ab-$\frac{1}{2}π{b}^{2}$. 已知一次函数y=kx+b的图象与x轴交于点A,与y轴交于点B(0,2),且与正比例函数y=$\frac{4}{3}$x的图象交于点C(m,4)
已知一次函数y=kx+b的图象与x轴交于点A,与y轴交于点B(0,2),且与正比例函数y=$\frac{4}{3}$x的图象交于点C(m,4)