Question

8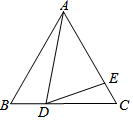．如图，在等边△ABC中，点D是BC边上一动点，且∠ADE=60°，
（1）求证：△ABD∽△DCE；
（2）若等边△ABC的边长为9，AE=7，求BD的长．

Answer 1

分析 （1）由在等边△ABC中，∠ADE=60°，易得∠B=∠C=60°，∠CDE=∠BAD，则可证得：△ABD∽△DCE；
（2）首先设BD=x，则CD=BC-CD=9-x，然后由△ABD∽△DCE，根据相似三角形的对应边成比例，即可求得答案．

解答 （1）证明：∵△ABC是等边三角形，
∴∠B=∠C=60°，
∵∠ADE+∠CDE=∠B+∠BAD，∠ADE=60°，
∴∠CDE=∠BAD，
∴△ABD∽△DCE；

（2）解：∵等边△ABC的边长为9，AE=7，
∴AB=BC=AC=9，
∴CE=2，
设BD=x，则CD=BC-CD=9-x，
∵△ABD∽△DCE，
∴$\frac{AB}{CD}$=$\frac{BD}{CE}$，
∴$\frac{9}{9-x}$=$\frac{x}{2}$，
解得：x=3或x=6．
∴BD的长为：3或6．

点评 此题考查了相似三角形的判定与性质以及等边三角形的性质．注意利用方程思想求解是关键．