Question

17．如图1，在△ABC中，∠ABC，∠ACB的角平分线交于点O，则∠BOC=90°+$\frac{1}{2}$∠A=$\frac{1}{2}$×180°+$\frac{1}{2}$∠A．如图2，在△ABC中，∠ABC，∠ACB的两条三等分角线分别对应交于O₁，O₂，则∠BO₁C=$\frac{2}{3}$×180°+$\frac{1}{3}$∠A，∠BO₂C=$\frac{1}{3}$×180°+$\frac{2}{3}$∠A．根据以上阅读理解，你能猜想（n等分时，内部有n-1个点）（用n的代数式表示）∠BO_n-1C=$\frac{1}{n}$×180°+$\frac{n-1}{n}$∠A．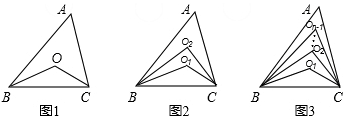 

Answer 1

分析 根据已知中的特例，观察两部分前边的倍数和n等分线间的关系，从而写出结论．

解答 解：根据题中所给的信息，总结可得：∠BO₁C=$\frac{n-1}{n}$×180°+$\frac{1}{n}$∠A，
∠BO_n-1C=$\frac{1}{n}$×180°+$\frac{n-1}{n}$∠A．
故答案为：$\frac{1}{n}$×180°+$\frac{n-1}{n}$∠A

点评 本题考查了三角形的内角和定理，综合运用了三角形的内角和定理和n等分角的概念，难度不大，注意由特殊到一般的总结．