题目内容
20.已知一元二次方程x2-2x+m=0(1)若方程有两个实数根,求m的范围;
(2)若方程的两个实数根为x1和x2,且x1+3x2=3,求m的值.
(3)若方程的两个实数根为x1和x2,且x12-x22=0,求m的值.
分析 (1)一元二次方程x2-2x+m=0有两个实数根,△≥0,把系数代入可求m的范围;
(2)利用两根关系,已知x1+x2=2结合x1+3x2=3,先求x1、x2,再求m;
(3)由x12-x22=0,利用平方差公式以及x1+x2=2可得x1-x2=0,则方程x2-2x+m=0有两个相等的实数根,△=(-2)2-4m=0,即可求出m=1.
解答 解:(1)∵方程x2-2x+m=0有两个实数根,
∴△=(-2)2-4m≥0,
解得m≤1;
(2)由两根关系可知,x1+x2=2,x1•x2=m,
解方程组$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=2}\\{{x}_{1}+3{x}_{2}=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{1}=\frac{3}{2}}\\{{x}_{2}=\frac{1}{2}}\end{array}\right.$,
∴m=x1•x2=$\frac{3}{2}$×$\frac{1}{2}$=$\frac{3}{4}$;
(3)∵x12-x22=0,
∴(x1+x2)(x1-x2)=0,
∵x1+x2=2≠0,
∴x1-x2=0,
∴方程x2-2x+m=0有两个相等的实数根,
∴△=(-2)2-4m=0,
解得m=1.
点评 本题考查了一元二次方程根与系数的关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的情况与判别式△的关系.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
10.若A($\frac{3}{4}$,y1),B(-$\frac{5}{4}$,y2),C(${\frac{1}{4}$,y3)为二次函数y=x2+4x-5的图象上的三点,则y1、y2、y3的大小关系是( )
| A. | y1<y2<y3 | B. | y2<y3<y1 | C. | y3<y1<y2 | D. | y1<y3<y2 |

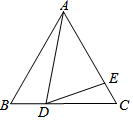 如图,在等边△ABC中,点D是BC边上一动点,且∠ADE=60°,
如图,在等边△ABC中,点D是BC边上一动点,且∠ADE=60°,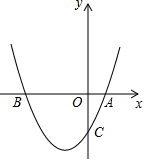 已知二次函数y=ax2+bx+c过点A(1,0),B(-3,0),C(0,-3)
已知二次函数y=ax2+bx+c过点A(1,0),B(-3,0),C(0,-3) 在矩形纸片ABCD中,AB=3,AD=5.如图所示,折叠纸片使点A落在边BC上的A'处,折痕为PQ.当点A'在边BC上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在边AB、AD上移动,则点B与点A'间的最小距离为1.
在矩形纸片ABCD中,AB=3,AD=5.如图所示,折叠纸片使点A落在边BC上的A'处,折痕为PQ.当点A'在边BC上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在边AB、AD上移动,则点B与点A'间的最小距离为1.