题目内容
10.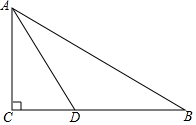 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D点,O是AB上一点,经过A、D两点的⊙O分别交AB、AC于点E、F.
如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D点,O是AB上一点,经过A、D两点的⊙O分别交AB、AC于点E、F.(1)用尺规补全图形(保留作图痕迹,不写作法);
(2)求证:BC与⊙O相切;
(3)当AD=$\sqrt{3}$,∠CAD=30°时,求劣弧AD的长.
分析 (1)作AD的垂直平分线交AC于O,以AO为半径画圆O分别交AB、AC于点E、F,则⊙O即为所求;
(2)连结OD,得到OD=OA,根据等腰三角形的性质得到∠OAD=∠ODA,等量代换得到∠ODA=∠CAD,根据平行线的判定定理得到OD∥AC,根据平行线的性质即可得到结论;
(3)连接DE,根据圆周角定理得到∠ADE=90°,根据三角形的内角和得到∠AOD=120°,根据三角函数的定义得到AE=2,根据弧长个公式即可得到结论.
解答 解:(1)如图所示,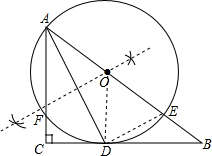
(2)证明:连结OD,则OD=OA,
∴∠OAD=∠ODA,
∵∠OAD=∠CAD,
∴∠ODA=∠CAD,
∴OD∥AC,
∵∠C=90°,
∴∠ODC=90°,
即BC⊥OD,
∴BC与⊙O相切;
(3)如图,连接DE,
∵AE是⊙O的直径,
∴∠ADE=90°,
∵∠OAD=∠ODA=30°,
∴∠AOD=120°,
在Rt△ADE中,AE=$\frac{AD}{cos∠EAD}$=2,
∴⊙O的半径=1,
∴劣弧AD的长=$\frac{120π×1}{180}$=$\frac{2}{3}$π.
点评 本题考查了切线的判定,圆周角定理,解直角三角形,弧长的计算,平行线的判定,基本作图,作出辅助线构造直角三角形是解本题的关键.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
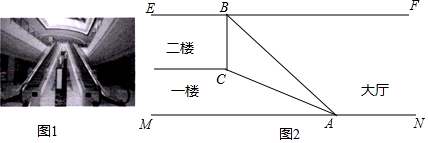
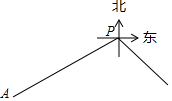 如图,甲船在港口P的南偏西60°方向,距港口86海里的A处,沿AP方向以每小时15海里的速度匀速行驶向港口P,乙船从港口P出发,沿南偏东45°方向匀速行驶驶离岗口P,现两船同时出发,2小时后乙船在甲船的正东方向,求乙船的航行速度(结果精确到个位,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236)
如图,甲船在港口P的南偏西60°方向,距港口86海里的A处,沿AP方向以每小时15海里的速度匀速行驶向港口P,乙船从港口P出发,沿南偏东45°方向匀速行驶驶离岗口P,现两船同时出发,2小时后乙船在甲船的正东方向,求乙船的航行速度(结果精确到个位,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236) 如图,在平面直角坐标系中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作直线l的垂线交y轴于点A1,以A1B、BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则C2017的坐标是(-$\sqrt{3}$×42016,42017).
如图,在平面直角坐标系中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作直线l的垂线交y轴于点A1,以A1B、BA为邻边作?ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1、B1A1为邻边作?A1B1A2C2;…;按此作法继续下去,则C2017的坐标是(-$\sqrt{3}$×42016,42017). 如图,数轴上有A、B、C、D四点,根据图中各点的位置,所表示的数与5-$\sqrt{11}$最接近的点是( )
如图,数轴上有A、B、C、D四点,根据图中各点的位置,所表示的数与5-$\sqrt{11}$最接近的点是( )