题目内容
18.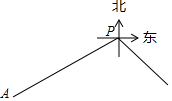 如图,甲船在港口P的南偏西60°方向,距港口86海里的A处,沿AP方向以每小时15海里的速度匀速行驶向港口P,乙船从港口P出发,沿南偏东45°方向匀速行驶驶离岗口P,现两船同时出发,2小时后乙船在甲船的正东方向,求乙船的航行速度(结果精确到个位,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236)
如图,甲船在港口P的南偏西60°方向,距港口86海里的A处,沿AP方向以每小时15海里的速度匀速行驶向港口P,乙船从港口P出发,沿南偏东45°方向匀速行驶驶离岗口P,现两船同时出发,2小时后乙船在甲船的正东方向,求乙船的航行速度(结果精确到个位,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236)
分析 设乙船的航行速度为每小时x海里,2小时后甲船在点B处,乙船在点C处,则PC=2x海里,过P作PD⊥BC于D,求出BP,在Rt△BPD中求出PD,然后在Rt△PDC中表示出PD,继而建立方程可解出x的值.
解答 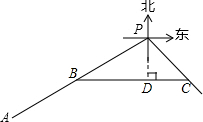 解:设乙船的航行速度为每小时x海里,2小时后甲船在点B处,乙船在点C处,则PC=2x海里,
解:设乙船的航行速度为每小时x海里,2小时后甲船在点B处,乙船在点C处,则PC=2x海里,
过P作PD⊥BC于D,则BP=86-2×15=56(海里),
在Rt△PDB中,∠PDB=90°,∠BPD=60°,
∴PD=PB•cos60°=28(海里),
在Rt△PDC中,∠PDC=90°,∠DPC=45°,
∴PD=PC•cos45°=2x•$\frac{\sqrt{2}}{2}$=$\sqrt{2}$x,
∴$\sqrt{2}$x=28,即x=14$\sqrt{2}$≈20,
答:乙船的航行速度约为每小时20海里.
点评 本题考查了解直角三角形的应用-方向角问题,解答本题的关键是构造直角三角形,能利用三角函数表示相关线段的长度,难度一般.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.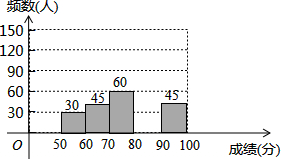 为了弘扬优秀传统文化,某中学举办了文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不扣分,赛后对全体参赛选手的答题情况进行了相关统计,整理并绘制成如下图表:
为了弘扬优秀传统文化,某中学举办了文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不扣分,赛后对全体参赛选手的答题情况进行了相关统计,整理并绘制成如下图表:
请根据以图表信息,解答下列问题:
(1)表中m=120,n=0.2;
(2)补全频数分布直方图;
(3)在得分前5名的同学中,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学参加区级的比赛,用树状图或列表法求选出的两名同学恰好是一男一女的概率.
 为了弘扬优秀传统文化,某中学举办了文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不扣分,赛后对全体参赛选手的答题情况进行了相关统计,整理并绘制成如下图表:
为了弘扬优秀传统文化,某中学举办了文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不扣分,赛后对全体参赛选手的答题情况进行了相关统计,整理并绘制成如下图表:| 组别 | 分数段 | 频数(人) | 频率 |
| 1 | 50≤x<60 | 30 | 0.1 |
| 2 | 60≤x<70 | 45 | 0.15 |
| 3 | 70≤x<80 | 60 | n |
| 4 | 80≤x<90 | m | 0.4 |
| 5 | 90≤x<100 | 45 | 0.15 |
(1)表中m=120,n=0.2;
(2)补全频数分布直方图;
(3)在得分前5名的同学中,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学参加区级的比赛,用树状图或列表法求选出的两名同学恰好是一男一女的概率.
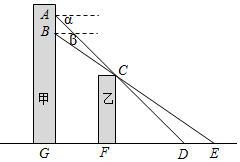 小张在甲楼A处向外看,由于受到前面乙楼的遮挡,最近只能看到地面D处,俯角为α.小颖在甲楼B处(B在A的正下方)向外看,最近能看到地面E处,俯角为β,地面上G,F,D,E在同一直线上,已知乙楼高CF为10m,甲乙两楼相距FG为15m,俯角α=45°,β=35°.
小张在甲楼A处向外看,由于受到前面乙楼的遮挡,最近只能看到地面D处,俯角为α.小颖在甲楼B处(B在A的正下方)向外看,最近能看到地面E处,俯角为β,地面上G,F,D,E在同一直线上,已知乙楼高CF为10m,甲乙两楼相距FG为15m,俯角α=45°,β=35°. 如图,AB是⊙O的直径,AB=15,AC=9,则cos∠ADC=$\frac{4}{5}$.
如图,AB是⊙O的直径,AB=15,AC=9,则cos∠ADC=$\frac{4}{5}$.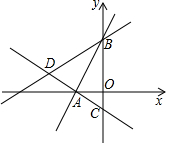 如图所示,在平面直角坐标系中,过点A(-$\sqrt{3}$,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2-2x-3=0的两个根
如图所示,在平面直角坐标系中,过点A(-$\sqrt{3}$,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2-2x-3=0的两个根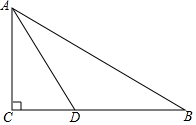 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D点,O是AB上一点,经过A、D两点的⊙O分别交AB、AC于点E、F.
如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于D点,O是AB上一点,经过A、D两点的⊙O分别交AB、AC于点E、F.