题目内容

15．求证：无论k取何值，关于x的一元二次方程x2-kx+（k-2）=0一定有两个不相等的实数根．

分析 先求出△的值，再根据△＞0，即可得出答案．

解答 证明：∵△=（-k）2-4（k-2）=k2-4k+8=（k-2）2+4＞0，
∴关于x的一元二次方程x2-kx+（k-2）=0一定有两个不相等的实数根．

点评 此题考查了根的判别式，一元二次方程ax2+bx+c=0（a≠0）的根与△=b2-4ac有如下关系：
①当△＞0时，方程有两个不相等的实数根；②当△=0时，方程有两个相等的实数根；③当△＜0时，方程无实数根．上面的结论反过来也成立．

练习册系列答案
相关题目
5．如图，在平面直角坐标系中，矩形OABC的四个顶点坐标分别为O（0，0），A（4，0），B（4，3），C（0，3），G是对角线AC的中点，动直线MN平行于AC且交矩形OABC的一组邻边于E、F，交y轴、x轴于M、N．设点M的坐标为（0，t）．

（1）当t=2时求△EFG的面积S；
（2）当△EFG为直角三角形时，求t的值；
（3）当点G关于直线EF的对称点G′恰好落在矩形OABC的一条边所在直线上时，直接y写出t的值．
6．（1）（2x+y）2-（4x+y）（y-x）
（2）（$\frac{3{y}^{2}}{x-y}$-x-y）÷$\frac{{x}^{2}-2xy}{{x}^{2}-xy}$．
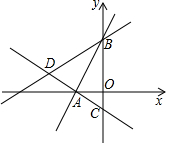3．如图所示，在平面直角坐标系中，过点A（-$\sqrt{3}$，0）的两条直线分别交y轴于B、C两点，且B、C两点的纵坐标分别是一元二次方程x2-2x-3=0的两个根
（Ⅰ）试问：直线AC与直线AB是否垂直？请说明理由；
（Ⅱ）若点D在直线AC上，且DB=DC，求点D的坐标；
（Ⅲ）在（Ⅱ）的条件下，在直线BD上寻找点P，使以A、B、P三点为顶点的三角形是等腰三角形，请直接写出P点的坐标．
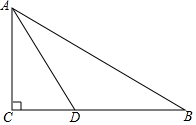10．如图，在Rt△ABC中，∠C=90°，AD平分∠CAB交BC于D点，O是AB上一点，经过A、D两点的⊙O分别交AB、AC于点E、F．
（1）用尺规补全图形（保留作图痕迹，不写作法）；
（2）求证：BC与⊙O相切；
（3）当AD=$\sqrt{3}$，∠CAD=30°时，求劣弧AD的长．
20．$\sqrt{{3}^{2}}$的立方根是（　　）
A．$\root{3}{3}$B．$\root{3}{9}$C．2D．3
7．分解因式：-2x3+4x2y-2xy2=-2x（x-y）2．
4．某校开展“阳光体育”活动，决定开设乒乓球、篮球、跑步、跳绳这四种运动项目，学生只能选择其中一种，为了解学生喜欢哪一种项目，随机抽取了部分学生进行调查，并将调查结果绘制成两张不完整的统计图，请你结合图中的信息解答下列问题：
（1）样本中喜欢篮球项目的人数百分比是20%；其所在扇形统计图中的圆心角的度数是72°；
（2）把条形统计图补画完整并注明人数；
（3）已知该校有1000名学生，根据样本估计全校喜欢乒乓球的人数是多少？
5．如图，正方形ABCD中，点E为对角线AC上一点，且AE=AB，则∠BED的度数是135度．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网