题目内容
8.已知x=$\sqrt{100×101×102×103+1}$-1012,则x=100.分析 设100=a,求出100×101×102×103+1=(a2+3a+1)2,再利用二次根式的性质,即可解答.
解答 解:设100=a,
100×101×102×103+1
=a(a+1)(a+2)(a+3)+1
=(a+3)a(a+1)(a+2)+1
=(a2+3a)(a2+3a+2)+1
=(a2+3a)2+2(a2+3a)+1
=(a2+3a+1)2
∴x=a2+3a+1-1012
=a2+2a+1+a-1012
=(a+1)2-1012+a
=1012-1012+100
=100.
故答案为:100.
点评 本题考查了二次根式的性质,解决本题的关键是熟记二次根式的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.二次函数y=ax2+bx+c(a,b,c为常数,a≠0)中,x与y的部分对应值如下表:
有下列结论:
①函数有最大值,且最大值为1;
②若x0满足y=ax02+bx+c,则2<x0<3或-1<x0<0;
③若方程ax2+bx+c+m=0有两个不等的实数根且m<-1;
④对于任意实数m,当m≠1时,有m(am+b)<$\frac{1}{2}$.
其中正确结论的个数是( )
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | -3.5 | -1 | 0.5 | 1 | 0.5 | -1 | -3.5 | … |
①函数有最大值,且最大值为1;
②若x0满足y=ax02+bx+c,则2<x0<3或-1<x0<0;
③若方程ax2+bx+c+m=0有两个不等的实数根且m<-1;
④对于任意实数m,当m≠1时,有m(am+b)<$\frac{1}{2}$.
其中正确结论的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
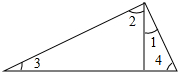 如图,已知∠1+∠2=90°,∠2+∠3=90°
如图,已知∠1+∠2=90°,∠2+∠3=90°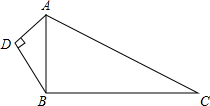 如图,已知AD=6,BD=8,AC=26,BC=24,∠ADB=90°.问△ABC是直角三角形吗?并说明理由.
如图,已知AD=6,BD=8,AC=26,BC=24,∠ADB=90°.问△ABC是直角三角形吗?并说明理由. 在中超联赛期间,一队员在距离球门12米处挑射,正好射中了2.4米高的横梁,已知球的最高点距球门的水平距离为3米,若足球运行的路线是抛物线,如图,求其函数解析式.
在中超联赛期间,一队员在距离球门12米处挑射,正好射中了2.4米高的横梁,已知球的最高点距球门的水平距离为3米,若足球运行的路线是抛物线,如图,求其函数解析式.