题目内容
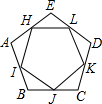 如图,H、I、J、K、L分别是正五边形ABCDE各边的中点,求证:五边形HIJKL是正五边形.
如图,H、I、J、K、L分别是正五边形ABCDE各边的中点,求证:五边形HIJKL是正五边形.考点:正多边形和圆
专题:证明题
分析:由H、I、J、K、L分别是正五边形ABCDE各边的中点,根据正五边形易证得∠A=∠B=∠C=∠D=∠E,AB=BC=CD=DE=AE,然后由等腰三角形的性质,可得AI=BI=BJ=CJ=CK=DK=DL=EL=EH=AH,继而证得∠HIJ=∠IJK=∠JKL=∠KLH=∠LHI,△AHI≌△BIJ≌△CIK≌△DKL≌△ELH(SAS).则可得TJ=JK=KL=HL=HI,即可证得结论.
解答:证明:∴五边形ABCDE是正五边形,
∴∠A=∠B=∠C=∠D=∠E,AB=BC=CD=DE=AE,
∵H、I、J、K、L分别是正五边形ABCDE各边的中点,
∴AI=BI=BJ=CJ=CK=DK=DL=EL=EH=AH,
∴∠AHI=∠AIH=∠BIJ=∠BJI=∠CJK=∠CKJ=∠DKL=∠DLK=∠ELH=∠EHL,
∴∠HIJ=∠IJK=∠JKL=∠KLH=∠LHI,
在△AHI和△BIJ和△CIK和△DKL和△ELH中,
,
∴△AHI≌△BIJ≌△CJK≌△DKL≌△ELH(SAS)
∴TJ=JK=KL=HL=HI,
∴五边形HIJKL是正五边形.
∴∠A=∠B=∠C=∠D=∠E,AB=BC=CD=DE=AE,
∵H、I、J、K、L分别是正五边形ABCDE各边的中点,
∴AI=BI=BJ=CJ=CK=DK=DL=EL=EH=AH,
∴∠AHI=∠AIH=∠BIJ=∠BJI=∠CJK=∠CKJ=∠DKL=∠DLK=∠ELH=∠EHL,
∴∠HIJ=∠IJK=∠JKL=∠KLH=∠LHI,
在△AHI和△BIJ和△CIK和△DKL和△ELH中,
|
∴△AHI≌△BIJ≌△CJK≌△DKL≌△ELH(SAS)
∴TJ=JK=KL=HL=HI,
∴五边形HIJKL是正五边形.
点评:此题考查了正五边形的性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
计算:
①0.25-
+(-1
)-(+3
)
②-105
÷(-
)
③-32+(-2
)2×(-
)+|-22|
④(-1)2013-{(-3)3-[3+
×(-1
)]÷(-2)}.
①0.25-
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
②-105
| 5 |
| 9 |
| 5 |
| 3 |
③-32+(-2
| 1 |
| 2 |
| 4 |
| 25 |
④(-1)2013-{(-3)3-[3+
| 2 |
| 3 |
| 1 |
| 2 |
 如图,小李打网球时,球恰好打过网,且落在离网4m的位置上,则球拍击球的高度h为( )
如图,小李打网球时,球恰好打过网,且落在离网4m的位置上,则球拍击球的高度h为( )| A、1.6m | B、1.5m |
| C、2.4m | D、1.2m |
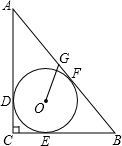 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,⊙O为△ABC内切圆,与三边分别相切于D、E、F.
如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,⊙O为△ABC内切圆,与三边分别相切于D、E、F. 如图,AD是△ABC的角平分线,过点D分别作AC和AB的平行线,交AB于点E,交AC于点F.求证:四边形AEDF是菱形.
如图,AD是△ABC的角平分线,过点D分别作AC和AB的平行线,交AB于点E,交AC于点F.求证:四边形AEDF是菱形.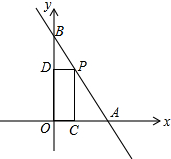 如图,一次函数y=-2x+3的图象交x轴于点A,交y轴于点B,点P在线段AB上(不与点A,B重合),过点P分别作OA和OB的垂线,垂足为C,D.点P在何处时,矩形OCPD的面积为1?
如图,一次函数y=-2x+3的图象交x轴于点A,交y轴于点B,点P在线段AB上(不与点A,B重合),过点P分别作OA和OB的垂线,垂足为C,D.点P在何处时,矩形OCPD的面积为1?