��Ŀ����
��ͼ��������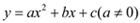 ��ͼ�����C��0��1��������ΪQ��2��3��,��D��x���������ϣ��߶�OD=OC.
��ͼ�����C��0��1��������ΪQ��2��3��,��D��x���������ϣ��߶�OD=OC.
��1���������ߵĽ���ʽ��
��2�����������Ƿ���ڵ�M��ʹ�á�CDM����CDΪֱ�DZߵ�ֱ�������Σ������ڣ������M������ꣻ�������ڣ���˵�����ɣ�
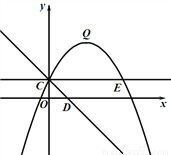
��3����ֱ��CD�Ƶ�C��ʱ�뷽����ת45������ֱ�����������ཻ����һ��E������QE.����P���߶�QE�ϵĶ��㣬��F���߶�OD�ϵĶ��㣬�ʣ���P���F����ƶ������У���PCF���ܳ��Ƿ������Сֵ�������ڣ���������Сֵ���������ڣ���˵������.
��ϰ��ϵ�д�
 ͬ����ϰ���ϴ�ѧ������ϵ�д�
ͬ����ϰ���ϴ�ѧ������ϵ�д� ͬ����ϰ���ϴ�ѧ������ϵ�д�
ͬ����ϰ���ϴ�ѧ������ϵ�д� ����ϰ�⽭��ϵ�д�
����ϰ�⽭��ϵ�д� ѧ���쳵��������������������ϵ�д�
ѧ���쳵��������������������ϵ�д�
�����Ŀ


 �����㲻�غ�
�����㲻�غ� ����ôͼ��
����ôͼ��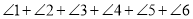 �Ķ�������
�Ķ�������
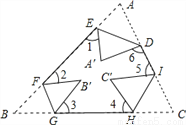
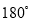
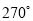
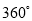
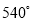
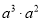 �Ľ����
�Ľ����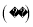
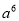 B.
B. 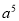 C.
C. 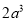 D. a
D. a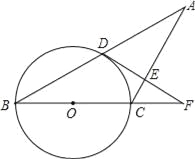
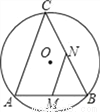
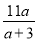 ������a=3��
������a=3��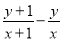 ��ֵ�ǣ�������
��ֵ�ǣ�������