题目内容
2.有A、B两个不透明的布袋,A袋中有三个相同的小球,分别标有数字-2,0和1,B袋中有两个相同的小球,分别标有数字0和-2,小林从A袋中随机取出一个小球,记录标有的数字为x,再从B袋中随机取出一个小球,记录标有的数字为y,这样确定了点Q的坐标(x,y)(1)用画树状图或列表的形式,求点Q在y轴上的概率;
(2)在平面直角坐标系xOy中,⊙O的半径是2,求过点Q能作⊙O切线的概率.
分析 (1)首先根据题意画出树状图,然后由树状图即可求得所有等可能的结果;再由点Q在y轴上的有:(-2,0),(0,0),(0,1)利用概率公式即可求得点Q在y轴上的概率;
(2)因为当点Q在圆上或在圆外时,过点Q能作⊙O切线,由在⊙O外的有(-2,1),(-2,-2),在⊙O上的有(0,-2),(-2,0),利用概率公式即可求得答案.
解答  解:(1)画树状图得:
解:(1)画树状图得:
则点Q所有可能的坐标有:(-2,0),(0,0),(1,0),(-2,-2),(0,-2),(1,-2);
∵点Q在y轴上的有:(0,-2),(0,0),
∴点Q在y轴上的概率为:$\frac{1}{3}$;
(2)∵⊙O的半径是2,
∴在⊙O外的有(-2,-2),(-2,1)在⊙O上的有(0,-2),(-2,0),
∴过点Q能作⊙O切线的概率为:$\frac{2}{3}$.
点评 此题考查了列表法与树状图法求概率的知识.此题难度适中,注意列表法与树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
17.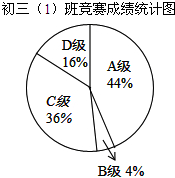 初三(1)班50人参加年级数学竞赛,成绩分为A,B,C,D四个等级,期中相应等级的得分为100分,90分,80分,70分,该班竞赛成绩的统计图如图,以下说法正确的是( )
初三(1)班50人参加年级数学竞赛,成绩分为A,B,C,D四个等级,期中相应等级的得分为100分,90分,80分,70分,该班竞赛成绩的统计图如图,以下说法正确的是( )
 初三(1)班50人参加年级数学竞赛,成绩分为A,B,C,D四个等级,期中相应等级的得分为100分,90分,80分,70分,该班竞赛成绩的统计图如图,以下说法正确的是( )
初三(1)班50人参加年级数学竞赛,成绩分为A,B,C,D四个等级,期中相应等级的得分为100分,90分,80分,70分,该班竞赛成绩的统计图如图,以下说法正确的是( )| A. | B级人数比A级人数少21 | B. | 50人得分的众数是22 | ||
| C. | 50人得分的平均数是80 | D. | 50人得分的中位数是80 |
7.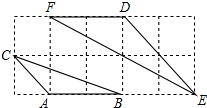 如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么△DEF与△ABC的周长比为( )
如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么△DEF与△ABC的周长比为( )
 如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么△DEF与△ABC的周长比为( )
如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么△DEF与△ABC的周长比为( )| A. | 4:1 | B. | 3:1 | C. | 2:1 | D. | $\sqrt{2}$:1 |
14.某学校抽查了某班级某月5天的用电量,数据如下表(单位:度):
(1)求这5天的用电量的平均数;
(2)求这5天用电量的众数、中位数;
(3)学校共有36个班级,若该月按22天计,试估计该校该月的总用电量.
| 度数 | 9 | 10 | 11 |
| 天数 | 3 | 1 | 1 |
(2)求这5天用电量的众数、中位数;
(3)学校共有36个班级,若该月按22天计,试估计该校该月的总用电量.
11.下列无理数中,在-1与2之间的是( )
| A. | -$\sqrt{3}$ | B. | -$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{5}$ |
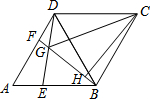 如图,△ADB、△BCD都是等边三角形,点E,F分别是AB,AD上两个动点,满足AE=DF.连接BF与DE相交于点G,CH⊥BF,垂足为H,连接CG.若DG=a,BG=b,且a、b满足下列关系:a2+b2=5,ab=2,则GH=$\frac{3}{2}$.
如图,△ADB、△BCD都是等边三角形,点E,F分别是AB,AD上两个动点,满足AE=DF.连接BF与DE相交于点G,CH⊥BF,垂足为H,连接CG.若DG=a,BG=b,且a、b满足下列关系:a2+b2=5,ab=2,则GH=$\frac{3}{2}$. 如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.
如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.