题目内容
12.将关于x的一元二次方程x2+px+q=0变形为x2=-px-q,就可将x2表示为关于x的一次多项式,从而达到“降次”的目的,我们称这样的方法为“降次法”,已知x2-x-1=0,可用“降次法”求得x4-3x+2014的值是2016.分析 先求得x2=x+1,再代入x4-3x+2014即可得出答案.
解答 解:∵x2-x-1=0,
∴x2=x+1,
∴x4-3x+2014=(x+1)2-3x+2014
=x2+2x+1-3x+2014
=x2-x+2015
=x+1-x+2015
=2016.
故答案为:2016.
点评 本题考查了一元二次方程的解,将四次先降为二次,再将二次降为一次,逐步得出答案即可.

练习册系列答案
相关题目
3.下列计算正确的是( )
| A. | a2×a3=a6 | B. | (a+b)2=a2+b2 | C. | (a+b)(a-b)=a2-b2 | D. | (a2)3=a5 |
7. 如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么△DEF与△ABC的周长比为( )
如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么△DEF与△ABC的周长比为( )
 如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么△DEF与△ABC的周长比为( )
如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么△DEF与△ABC的周长比为( )| A. | 4:1 | B. | 3:1 | C. | 2:1 | D. | $\sqrt{2}$:1 |
17.在函数y=$\sqrt{1-2x}$中,自变量x的取值范围是( )
| A. | x<$\frac{1}{2}$ | B. | x≤$\frac{1}{2}$ | C. | x>$\frac{1}{2}$ | D. | x≥$\frac{1}{2}$ |
4.下列运算正确的是( )
| A. | a3+a3=a6 | B. | 2(a+1)=2a+1 | C. | (-ab)2=a2b2 | D. | a6÷a3=a2 |
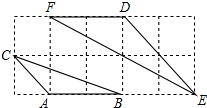
 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②PQ∥AE;③AC=BQ;④DE=DP;⑤CP=CQ;⑥∠AOB=60°.
如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②PQ∥AE;③AC=BQ;④DE=DP;⑤CP=CQ;⑥∠AOB=60°.