题目内容
17.解方程组:$\left\{\begin{array}{l}{x+2y=8,①}\\{{x}^{2}-5xy-6{y}^{2}=0②}\end{array}\right.$.分析 把方程②通过因式分解化为两个二元一次方程,把这两个方程分别与①组成方程组,解方程组得到答案.
解答 解:由②得,x+y=0,x-6y=0,
得到方程组$\left\{\begin{array}{l}{x+2y=8}\\{x+y=0}\end{array}\right.$,$\left\{\begin{array}{l}{x+2y=8}\\{x-6y=0}\end{array}\right.$,
第一个方程组的解为:$\left\{\begin{array}{l}{x=-8}\\{y=8}\end{array}\right.$,
第二个方程组的解为:$\left\{\begin{array}{l}{x=6}\\{y=1}\end{array}\right.$.
所以方程组的解:$\left\{\begin{array}{l}{x=-8}\\{y=8}\end{array}\right.$,$\left\{\begin{array}{l}{x=6}\\{y=1}\end{array}\right.$.
点评 本题考查的是二元二次方程组的解法,通过因式分解把其中的二元二次方程化为两个二元一次方程是解题的关键,本题也可以用代入法解方程组.

练习册系列答案
相关题目
7.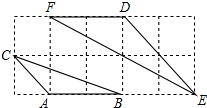 如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么△DEF与△ABC的周长比为( )
如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么△DEF与△ABC的周长比为( )
 如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么△DEF与△ABC的周长比为( )
如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么△DEF与△ABC的周长比为( )| A. | 4:1 | B. | 3:1 | C. | 2:1 | D. | $\sqrt{2}$:1 |
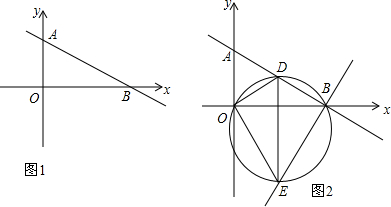
 如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.
如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.