题目内容
14.反比例函数y=$\frac{5}{x}$的图象上有A(-2,y1)、B(-1,y2)、C(1,y3)三点.试比较y1、y2、y3的大小.分析 根据反比例函数图象上点的坐标特征得到-2y1=5,-1×y2=5,1×y3=5,然后分别计算出y1、y2、y3的值后比较大小即可.
解答 解:∵反比例函数y=$\frac{5}{x}$的图象上有A(-2,y1)、B(-1,y2)、C(1,y3)三点,
∴-2y1=5,-1×y2=5,1×y3=5,
∴y1=-$\frac{5}{2}$,y2=-5,y3=5,
∴y2<y1<y3.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
4.若二次函数y=ax2+ax-1的最小值为-$\frac{7}{4}$,则a的值是( )
| A. | -1 | B. | 0 | C. | 3 | D. | 3或-1 |
15.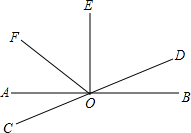 如图,直线AB、CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠BOD=15°,则下列结论中不正确的是( )
如图,直线AB、CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠BOD=15°,则下列结论中不正确的是( )
 如图,直线AB、CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠BOD=15°,则下列结论中不正确的是( )
如图,直线AB、CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠BOD=15°,则下列结论中不正确的是( )| A. | ∠AOF=45° | B. | ∠AOD与∠BOD互为补角 | ||
| C. | ∠BOD=∠AOC | D. | ∠BOD的余角等于85° |