题目内容
6.计算:(1)$\frac{-17{x}^{2}y}{54{a}^{2}b}$•$\frac{9a{b}^{3}}{-51xy}$
(2)(x2+6x+9)•$\frac{x+3}{{x}^{2}+9x+18}$.
分析 (1)直接约分求解即可,
(2)先因式分解,再约分求解即可.
解答 解:(1)$\frac{-17{x}^{2}y}{54{a}^{2}b}$•$\frac{9a{b}^{3}}{-51xy}$=$\frac{x{b}^{2}}{18a}$;
(2)(x2+6x+9)•$\frac{x+3}{{x}^{2}+9x+18}$=(x+3)2×$\frac{x+3}{(x+6)(x+3)}$=$\frac{(x+3)^{2}}{x+6}$.
点评 本题主要考查了分式的乘除法,解题的关键是正确的约分化简.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
16.某防疫站对某地区30 000名中小学生(高中生9000名,初中生10 000名,小学生11 000名)的身体健康情况进行调查,计划抽取100名初中学生进行抽样调查,则应抽取的高中学生为( )
| A. | 90 | B. | 110 | C. | 200 | D. | 300 |
15.若“!”是一种运算符号,并且1!=1,2!=2×1,3!=3×2×1,…,则$\frac{99!}{97!}$=( )
| A. | $\frac{99}{97}$ | B. | 98! | C. | 9702 | D. | 2! |
7.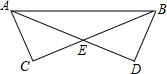 已知:如图,△ABC和△BAD中,AD=BC,要使△ABC≌△BAD,则下列添加的条件错误的是( )
已知:如图,△ABC和△BAD中,AD=BC,要使△ABC≌△BAD,则下列添加的条件错误的是( )
 已知:如图,△ABC和△BAD中,AD=BC,要使△ABC≌△BAD,则下列添加的条件错误的是( )
已知:如图,△ABC和△BAD中,AD=BC,要使△ABC≌△BAD,则下列添加的条件错误的是( )| A. | ∠ABC=∠BAD | B. | AC=BD | C. | ∠CAB=∠DBA | D. | ∠C=∠D=90° |
 如图,一滴墨水洒在一条数轴上,根据图中标出的数值判断墨迹盖住的整数的值有多少个?
如图,一滴墨水洒在一条数轴上,根据图中标出的数值判断墨迹盖住的整数的值有多少个?