题目内容
5.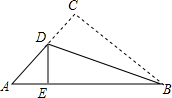 如图,在△ABC中,AB=8,BC=6,AC=5,点D在AC上,连结BD,将△ABC沿BD翻折后,若点C恰好落在AB边上的点E处,则△ADE的周长为7.
如图,在△ABC中,AB=8,BC=6,AC=5,点D在AC上,连结BD,将△ABC沿BD翻折后,若点C恰好落在AB边上的点E处,则△ADE的周长为7.
分析 由翻折的性质可知:DC=DE,BC=EB,于是可得到AD+DE=5,AE=2,故此可求得△ADE的周长为7.
解答 解:∵由翻折的性质可知:DC=DE,BC=EB=6.
∴AD+DE=AD+DC=AC=5,AE=AB-BE=AB-CB=8-6=2.
∴△ADE的周长=5+2=7.
故答案为:7.
点评 本题主要考查的是翻折的性质,根据翻折的性质求得AD+DE=5,AE=2是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.下列各式是完全平方式的是( )
| A. | x2+2x-1 | B. | 1+x2 | C. | x+xy+1 | D. | x2-2x+1 |
10.已知方程组$\left\{\begin{array}{l}{a+2b=4}\\{3a+2b=8}\end{array}\right.$,则点(a,b)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.正三角形ABC的内切圆半径为1,则△ABC的边长是( )
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 4 |
 如图,点D在AE上,BD=CD,∠BDE=∠CDE.求证:AB=AC.
如图,点D在AE上,BD=CD,∠BDE=∠CDE.求证:AB=AC.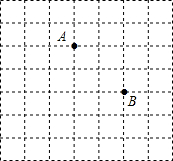 在某旅游景点,为了增加旅游的乐趣,特安排了一次“寻宝”游戏,寻宝人找到了如图所示的两个标志点A(2,1),B(4,-1),这两个标志点到“宝藏”点的距离都是$\sqrt{10}$,请你想想办法,在如图的方格纸中画出这个平面直角坐标系,并求出“宝藏”所在位置的坐标.
在某旅游景点,为了增加旅游的乐趣,特安排了一次“寻宝”游戏,寻宝人找到了如图所示的两个标志点A(2,1),B(4,-1),这两个标志点到“宝藏”点的距离都是$\sqrt{10}$,请你想想办法,在如图的方格纸中画出这个平面直角坐标系,并求出“宝藏”所在位置的坐标.