题目内容
7.已知方程2(m+1)x2+4mx+3m=2有两个不相等的实数根,求m的取值范围.分析 一元二次方程有两不等实数根,则根的判别式△=b2-4ac>0,建立关于m的不等式,求出m的取值范围.还要注意二次项系数不为0.
解答 解:(1)∵关于x的一元二次方程2(m+1)x2+4mx+3m-2=0 有两个不相等的实数根,
∴m+1≠0且△>0,
∵△=(4m)2-4×2(m+1)(3m-2)=-8m2-8m+16
∴-8m2-8m+16>0.
解得:-2<m<1,
∴m的取值范围是-2<m<1且m≠-1.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
15.正三角形ABC的内切圆半径为1,则△ABC的边长是( )
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 4 |
2.5-3的值是( )
| A. | 5 | B. | 2 | C. | -2 | D. | 3 |
19.下列从左到右的变形是因式分解的是( )
| A. | (2x+1)(2x-1)=4x2-1 | B. | a2-3a-4=a(a-3)-4 | C. | 8x5y2=4x3y2•2x2 | D. | m(n-1)-(n-1)=(m-1)(n-1) |
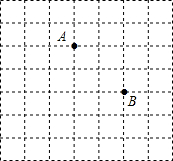 在某旅游景点,为了增加旅游的乐趣,特安排了一次“寻宝”游戏,寻宝人找到了如图所示的两个标志点A(2,1),B(4,-1),这两个标志点到“宝藏”点的距离都是$\sqrt{10}$,请你想想办法,在如图的方格纸中画出这个平面直角坐标系,并求出“宝藏”所在位置的坐标.
在某旅游景点,为了增加旅游的乐趣,特安排了一次“寻宝”游戏,寻宝人找到了如图所示的两个标志点A(2,1),B(4,-1),这两个标志点到“宝藏”点的距离都是$\sqrt{10}$,请你想想办法,在如图的方格纸中画出这个平面直角坐标系,并求出“宝藏”所在位置的坐标. 如图,铅球投掷场地呈扇形,其中投掷区的角度为40°,则这个角的余角为50°,补角为140°.
如图,铅球投掷场地呈扇形,其中投掷区的角度为40°,则这个角的余角为50°,补角为140°.