题目内容
4.在一个不透明的盒子中放有四张分别写有数字1、2、3、4的红色卡片和三张分别写有1、2、3的蓝色卡片,卡片除颜色和数字外其它完全相同.(1)从中任意抽取一张卡片,求该卡片上写有数字1的概率;
(2)将3张蓝色卡片取出后放入另外一个不透明的盒子内,然后在两个盒子内各任意抽取一张卡片,以红色卡片上的数字作为十位数,蓝色卡片上的数字作为个位数组成一个两位数,求这个两位数不小于22的概率(请利用树状图或列表法说明)
分析 (1)由在7张卡片中共有两张卡片写有数字1,利用概率公式求解即可求得答案;
(2)首先根据题意列出表格,然后由表格求得所有等可能的结果与这个两位数不小于22的情况,再利用概率公式求解即可求得答案.
解答 解:(1)∵在7张卡片中共有两张卡片写有数字1,
∴从中任意抽取一张卡片,卡片上写有数字1的概率是$\frac{2}{7}$;
(2)组成的所有两位数列表得:
| 1 | 2 | 3 | 4 | |
| 1 | 11 | 21 | 31 | 41 |
| 2 | 12 | 22 | 32 | 42 |
| 3 | 13 | 23 | 33 | 43 |
∴这个两位数不小于22的概率为:$\frac{8}{12}$=$\frac{2}{3}$.
点评 此题考查的是用列表法或树状图法求概率.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
12.为了解某校八、九年级部分学生的睡眠情况,随机抽取了该校八、九年级部分学生进行调查,已知抽取的八年级与九年级的学生人数相同,利用抽样所得的数据绘制如图的统计图表:
睡眠情况分段情况如下
根据图表提供的信息,回答下列问题:
(Ⅰ)直接写出统计图中a的值5%;
(Ⅱ)睡眠时间少于6.5小时为严重睡眠不足,则从该校八、九年级各随机抽一名学生,被抽到的这两位学生睡眠严重不足的可能性分别有多大?
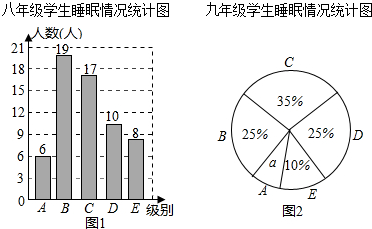
睡眠情况分段情况如下
| 组别 | 睡眠时间x(小时) |
| A | 4.5≤x<5.5 |
| B | 5.5≤x<6.5 |
| C | 6.5≤x<7.5 |
| D | 7.5≤x<8.5 |
| E | 8.5≤x<9.5 |
(Ⅰ)直接写出统计图中a的值5%;
(Ⅱ)睡眠时间少于6.5小时为严重睡眠不足,则从该校八、九年级各随机抽一名学生,被抽到的这两位学生睡眠严重不足的可能性分别有多大?

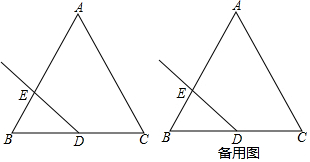
9.在四张完全相同的卡片上,分别画有圆、菱形、等腰三角形正六边形,现从中随机抽取一张,卡片上的图形是中心对称图形的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
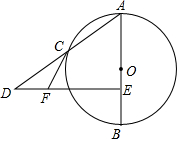 如图,已知AB是⊙O的直径,点C在⊙O上,点E在AB上,作DE⊥AB交AC的延长线于点D,过点C作⊙O的切线CF交DE于点F.
如图,已知AB是⊙O的直径,点C在⊙O上,点E在AB上,作DE⊥AB交AC的延长线于点D,过点C作⊙O的切线CF交DE于点F. 如图,在大楼AB的正前方有一斜坡CD,已知斜坡CD长6$\sqrt{2}$米,坡角∠DCE等于45°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的顶点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.
如图,在大楼AB的正前方有一斜坡CD,已知斜坡CD长6$\sqrt{2}$米,坡角∠DCE等于45°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的顶点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.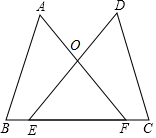 已知:如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.
已知:如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.