题目内容
16. 如图,在大楼AB的正前方有一斜坡CD,已知斜坡CD长6$\sqrt{2}$米,坡角∠DCE等于45°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的顶点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.
如图,在大楼AB的正前方有一斜坡CD,已知斜坡CD长6$\sqrt{2}$米,坡角∠DCE等于45°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的顶点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号).
分析 (1)在直角三角形DCE中,利用锐角三角函数定义求出DE的长即可;
(2)过D作DF垂直于AB,交AB于点F,可得出三角形BDF为等腰直角三角形,设AB=x米,则BF=(x-6)米,AC=(x-12)米,在Rt△ABC中,利用三角函数即可列方、方程求得x的值.
解答 解:(1)在Rt△DCE中,DC=6$\sqrt{2}$米,∠DCE=30°,∠DEC=90°,
∴DE=EC=6米;
(2)过D作DF⊥AB,交AB于点F,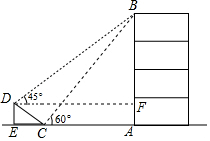
∵∠BFD=90°,∠BDF=45°,
∴∠BFD=45°,即△BFD为等腰直角三角形,则DF=BF,
设AB=x米,则BF=(x-6)米.
∵四边形DEAF为矩形,
∴AF=DE=6米,即AB=BF=(x-6)米,AC=(x-12)米,
在Rt△ABC中,∠ABC=30°,
tan30°=$\frac{AC}{AB}$,即$\frac{\sqrt{3}}{3}$=$\frac{x-12}{x}$,
解得:x=18+6$\sqrt{3}$,
即大楼的高度是18+6$\sqrt{3}$米.
点评 此题考查了解直角三角形-仰角俯角问题,坡度坡角问题,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
6.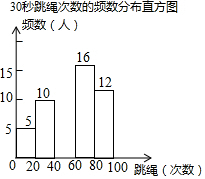 某校为迎接体育中考,了解学生的体育情况,学校随机调查了本校九年级50名学生“30秒跳绳”的次数,并将调查所得的数据整理如下:
某校为迎接体育中考,了解学生的体育情况,学校随机调查了本校九年级50名学生“30秒跳绳”的次数,并将调查所得的数据整理如下:
30秒跳绳次数的频数、频率分布表
根据以上图表信息,解答下列问题:
(1)表中的a=0.2,m=16;
(2)请把频数分布直方图补充完整;(画图后请标注相应的数据)
(3)若该校九年级共有600名学生,请你估计“30秒跳绳”的次数60次以上(含60次)的学生有多少人?
 某校为迎接体育中考,了解学生的体育情况,学校随机调查了本校九年级50名学生“30秒跳绳”的次数,并将调查所得的数据整理如下:
某校为迎接体育中考,了解学生的体育情况,学校随机调查了本校九年级50名学生“30秒跳绳”的次数,并将调查所得的数据整理如下:30秒跳绳次数的频数、频率分布表
| 成绩段 | 频数 | 频率 |
| 0≤x<20 | 5 | 0.1 |
| 20≤x<40 | 10 | a |
| 40≤x<60 | b | 0.14 |
| 60≤x<80 | m | c |
| 80≤x<100 | 12 | n |
(1)表中的a=0.2,m=16;
(2)请把频数分布直方图补充完整;(画图后请标注相应的数据)
(3)若该校九年级共有600名学生,请你估计“30秒跳绳”的次数60次以上(含60次)的学生有多少人?
6.2016年,义乌市经济总体平稳,全年实现地区生产总值1118亿元.将1118亿元用科学记数法表示应为(单位:元)( )
| A. | 1.118×103 | B. | 1.118×1010 | C. | 1.118×1011 | D. | 1.118×1012 |

 为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=21m,∠BAC=53°,求这颗古杉树AB的长度.
为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=21m,∠BAC=53°,求这颗古杉树AB的长度. 如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.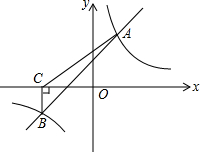 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,4)、B(-4,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,4)、B(-4,n)两点.