题目内容
15.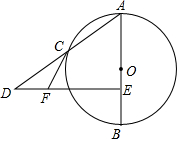 如图,已知AB是⊙O的直径,点C在⊙O上,点E在AB上,作DE⊥AB交AC的延长线于点D,过点C作⊙O的切线CF交DE于点F.
如图,已知AB是⊙O的直径,点C在⊙O上,点E在AB上,作DE⊥AB交AC的延长线于点D,过点C作⊙O的切线CF交DE于点F.(1)求证:CF=DF;
(2)若AB=10,BE=2.8,sin∠ADE=$\frac{3}{5}$,求CF的长.
分析 (1)连接OC,如图,利用切线的性质得∠OCF=90°,则∠1+∠2=90°,再利用∠1=∠A和互余可得到∠2=∠D,所以FC=FD;
(2)连接BC交DE于G,如图,利用圆周角定理得到∠ACB=90°,则∠D=∠B,利用三角函数,在Rt△ADE中,计算出AD=12,在Rt△ACB中计算出AC=6,则CD=6,接着利用sinD=$\frac{CG}{DG}$=$\frac{3}{5}$设CG=3x,则DG=5x,CD=4x,于是可计算出x=$\frac{3}{2}$,最好证明FC=FD=FG,于是得到DF=$\frac{1}{2}$DG=$\frac{15}{4}$.
解答 (1)证明:连接OC,如图,
∵CF为切线,
∴OC⊥CF,
∴∠OCF=90°,
∴∠1+∠2=90°,
∵OA=OC,
∴∠1=∠A,
∴∠A+∠2=90°,
而DE⊥AE,
∴∠D+∠A=90°,
∴∠2=∠D,
∴FC=FD;
(2)解:连接BC交DE于G,如图,
∵AB为直径,
∴∠ACB=90°,
∴∠D=∠B,
∵AB=10,BE=2.8,
∴AE=7.2,
在Rt△ADE中,∵sin∠ADE=$\frac{AE}{AD}$=$\frac{3}{5}$,
∴AD=$\frac{7.2}{\frac{3}{5}}$=12,
在Rt△ACB中,sinB=$\frac{AC}{AB}$=$\frac{3}{5}$,
∴AC=$\frac{3}{5}$×10=6,
∴CD=12-6=6,
∵∠D+∠DGC=90°,∠2+∠FCG=90°,
∴∠FGC=∠FCG,
∴CF=DF=FG,
在Rt△CDG,sinD=$\frac{CG}{DG}$=$\frac{3}{5}$,
设CG=3x,则DG=5x,
∴CD=4x,
∴4x=6,解得x=$\frac{3}{2}$,
∴DG=5x=$\frac{15}{2}$,
∴DF=$\frac{1}{2}$DG=$\frac{15}{4}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了解直角三角形.

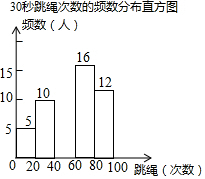 某校为迎接体育中考,了解学生的体育情况,学校随机调查了本校九年级50名学生“30秒跳绳”的次数,并将调查所得的数据整理如下:
某校为迎接体育中考,了解学生的体育情况,学校随机调查了本校九年级50名学生“30秒跳绳”的次数,并将调查所得的数据整理如下:30秒跳绳次数的频数、频率分布表
| 成绩段 | 频数 | 频率 |
| 0≤x<20 | 5 | 0.1 |
| 20≤x<40 | 10 | a |
| 40≤x<60 | b | 0.14 |
| 60≤x<80 | m | c |
| 80≤x<100 | 12 | n |
(1)表中的a=0.2,m=16;
(2)请把频数分布直方图补充完整;(画图后请标注相应的数据)
(3)若该校九年级共有600名学生,请你估计“30秒跳绳”的次数60次以上(含60次)的学生有多少人?


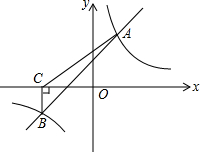 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,4)、B(-4,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,4)、B(-4,n)两点.