题目内容
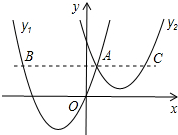 如图,抛物线y1=a(x+2)2-3与y2=
如图,抛物线y1=a(x+2)2-3与y2=| 1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:二次函数图象与几何变换
专题:
分析:根据与y2=
(x-3)2+1的图象在x轴上方即可得出y2的取值范围;把A(1,3)代入抛物线y1=a(x+2)2-3即可得出a的值;根据两函数的解析式直接得出AB与AC的关系即可.
| 1 |
| 2 |
解答:解:①∵抛物线y2=
(x-3)2+1开口向上,顶点坐标在x轴的上方,
∴无论x取何值,y2的值总是正数,故①正确;
②把A(1,3)代入,抛物线y1=a(x+2)2-3得,3=a(1+2)2-3,解得a=
,故②错误;
③由②知,a=
则
(x+2)2-3=
(x-3)2+1,
整理,得
x2+34x-35=0.
则△=342-4×1×(-35)=1296>0,
则y1与y2共有2个交点.
故③错误.
④∵物线y1=a(x+2)2-3与y2=
(x-3)2+1交于点A(1,3),
∴y1的对称轴为x=-2,y2的对称轴为x=3,
∴B(-5,3),C(5,3)
∴AB=6,AC=4,
∴2AB=3AC,故④正确.
综上所述,正确的结论是①④,共2个.
故选:B.
| 1 |
| 2 |
∴无论x取何值,y2的值总是正数,故①正确;
②把A(1,3)代入,抛物线y1=a(x+2)2-3得,3=a(1+2)2-3,解得a=
| 2 |
| 3 |
③由②知,a=
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
整理,得
x2+34x-35=0.
则△=342-4×1×(-35)=1296>0,
则y1与y2共有2个交点.
故③错误.
④∵物线y1=a(x+2)2-3与y2=
| 1 |
| 2 |
∴y1的对称轴为x=-2,y2的对称轴为x=3,
∴B(-5,3),C(5,3)
∴AB=6,AC=4,
∴2AB=3AC,故④正确.
综上所述,正确的结论是①④,共2个.
故选:B.
点评:本题考查的是二次函数的性质,根据题意利用数形结合进行解答是解答此题的关键,同时要熟悉二次函数图象上点的坐标特征.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
若关于x的方程2mx-3=1的解为x=2,则m的值为( )
| A、1 | B、-1 |
| C、0.5 | D、-0.5 |
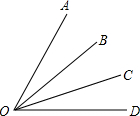 如图,射线OB、OC将∠AOD分成三部分,下列判断错误的是( )
如图,射线OB、OC将∠AOD分成三部分,下列判断错误的是( )| A、如果∠AOB=∠COD,那么∠AOC=∠BOD |
| B、如果∠AOB>∠COD,那么∠AOC>∠BOD |
| C、如果∠AOB<∠COD,那么∠AOC<∠BOD |
| D、如果∠AOB=∠BOC,那么∠AOC=∠BOD |
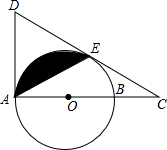 如图,AB是⊙的直径,AD切⊙O于A,延长AB到C,过C作⊙O的切线CE,切点为E,CE的延长线交AD于D,连接AE,且AE=CE.
如图,AB是⊙的直径,AD切⊙O于A,延长AB到C,过C作⊙O的切线CE,切点为E,CE的延长线交AD于D,连接AE,且AE=CE.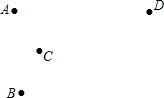 A、B、C、D四点的位置如图所示,按下列要求作图(不写作法,保留作图痕迹)
A、B、C、D四点的位置如图所示,按下列要求作图(不写作法,保留作图痕迹)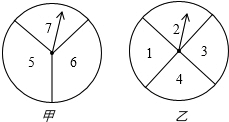 如图,两个转盘中指针落在每一个数字上的机会均等,转动甲、乙两个转盘,转盘停止后指针将各指向一个数字.
如图,两个转盘中指针落在每一个数字上的机会均等,转动甲、乙两个转盘,转盘停止后指针将各指向一个数字.