题目内容
7.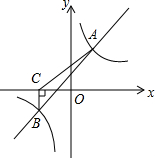 如图所示,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,4),B(-4,n)两点.
如图所示,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,4),B(-4,n)两点.(1)分别求出一次函数与反比例函数的表达式;
(2)过点B作BC⊥x轴,垂足为点C,连接AC,求△ACB的面积.
分析 (1)将点A坐标代入y=$\frac{m}{x}$可得反比例函数解析式,据此求得点B坐标,根据A、B两点坐标可得直线解析式;
(2)根据点B坐标可得底边BC=2,由A、B两点的横坐标可得BC边上的高,据此可得.
解答 解:(1)将点A(2,4)代入y=$\frac{m}{x}$,得:m=8,
则反比例函数解析式为y=$\frac{8}{x}$,
当x=-4时,y=-2,
则点B(-4,-2),
将点A(2,4)、B(-4,-2)代入y=kx+b,
得:$\left\{\begin{array}{l}{2k+b=4}\\{-4k+b=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$,
则一次函数解析式为y=x+2;
(2)由题意知BC=2,
则△ACB的面积=$\frac{1}{2}$×2×6=6.
点评 本题主要考查一次函数与反比例函数的交点问题,熟练掌握待定系数法求函数解析式及三角形的面积求法是解题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
18.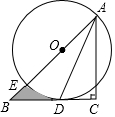 如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.
如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.
(1)求证:AD平分∠BAC;
(2)若CD=1,求图中阴影部分的面积(结果保留π).
 如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.
如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.(1)求证:AD平分∠BAC;
(2)若CD=1,求图中阴影部分的面积(结果保留π).
12.下列命题中假命题是( )
| A. | 正六边形的外角和等于360° | B. | 位似图形必定相似 | ||
| C. | 样本方差越大,数据波动越小 | D. | 方程x2+x+1=0无实数根 |
 如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD交△ABC的外接圆O于点E,连接AE.
如图,在四边形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,过点C作CE∥AD交△ABC的外接圆O于点E,连接AE.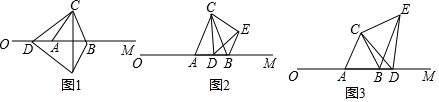

 ”的个数是3n+1.(用含有n的代数式表示)
”的个数是3n+1.(用含有n的代数式表示)