题目内容
19.已知,在Rt△ABC中,∠ACB=90°,AC=4,BC=2,D是AC边上的一个动点,将△ABD沿BD所在直线折叠,使点A落在点P处.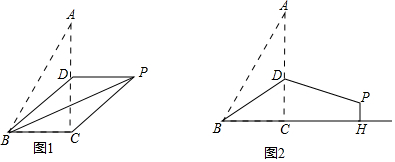
(1)如图1,若点D是AC中点,连接PC.
①写出BP,BD的长;
②求证:四边形BCPD是平行四边形.
(2)如图2,若BD=AD,过点P作PH⊥BC交BC的延长线于点H,求PH的长.
分析 (1)①分别在Rt△ABC,Rt△BDC中,求出AB、BD即可解决问题;
②想办法证明DP∥BC,DP=BC即可;
(2)如图2中,作DN⊥AB于N,PE⊥AC于E,延长BD交PA于M.设BD=AD=x,则CD=4-x,在Rt△BDC中,可得x2=(4-x)2+22,推出x=$\frac{5}{2}$,推出DN=$\sqrt{B{D}^{2}-B{N}^{2}}$=$\frac{\sqrt{5}}{2}$,由△BDN∽△BAM,可得$\frac{DN}{AM}$=$\frac{BD}{AB}$,由此求出AM,由△ADM∽△APE,可得$\frac{AM}{AE}$=$\frac{AD}{AP}$,由此求出AE=$\frac{16}{5}$,可得EC=AC-AE=4-$\frac{16}{5}$=$\frac{4}{5}$由此即可解决问题.
解答 解:(1)①在Rt△ABC中,∵BC=2,AC=4,
∴AB=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∵AD=CD=2,
∴BD=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
由翻折可知,BP=BA=2$\sqrt{5}$.
②如图1中,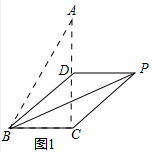
∵△BCD是等腰直角三角形,
∴∠BDC=45°,
∴∠ADB=∠BDP=135°,
∴∠PDC=135°-45°=90°,
∴∠BCD=∠PDC=90°,
∴DP∥BC,∵PD=AD=BC=2,
∴四边形BCPD是平行四边形.
(2)如图2中,作DN⊥AB于N,PE⊥AC于E,延长BD交PA于M.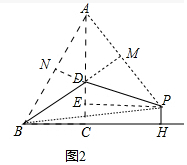
设BD=AD=x,则CD=4-x,
在Rt△BDC中,∵BD2=CD2+BC2,
∴x2=(4-x)2+22,
∴x=$\frac{5}{2}$,
∵DB=DA,DN⊥AB,
∴BN=AN=$\sqrt{5}$,
在Rt△BDN中,DN=$\sqrt{B{D}^{2}-B{N}^{2}}$=$\frac{\sqrt{5}}{2}$,
由△BDN∽△BAM,可得$\frac{DN}{AM}$=$\frac{BD}{AB}$,
∴$\frac{\frac{\sqrt{5}}{2}}{AM}$=$\frac{\frac{5}{2}}{2\sqrt{5}}$,
∴AM=2,
∴AP=2AM=4,
由△ADM∽△APE,可得$\frac{AM}{AE}$=$\frac{AD}{AP}$,
∴$\frac{2}{AE}$=$\frac{\frac{5}{2}}{4}$,
∴AE=$\frac{16}{5}$,
∴EC=AC-AE=4-$\frac{16}{5}$=$\frac{4}{5}$,
易证四边形PECH是矩形,
∴PH=EC=$\frac{4}{5}$.
点评 本题考查四边形综合题、勾股定理.相似三角形的判定和性质、翻折变换、等腰三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造相似三角形解决问题,属于中考压轴题.

| x(元/件) | 10 | 12 | 14 | 16 |
| y(件) | 200 | 180 | 160 | 140 |
(2)为使商场每周获得最大利润,试问这种背心定价应为多少?最大利利润是多少?
(3)若商场每周想要获得不低于1050元的利润,试确定这种儿童背心的定价x(元/件)的取值范围.
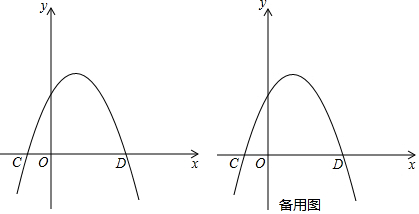
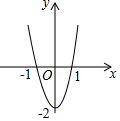 将如图所示的抛物线向右平移1个单位长度,再向上平移3个单位长度后,得到的抛物线解析式是( )
将如图所示的抛物线向右平移1个单位长度,再向上平移3个单位长度后,得到的抛物线解析式是( )| A. | y=(x-1)2+1 | B. | y=(x+1)2+1 | C. | y=2(x-1)2+1 | D. | y=2(x+1)2+1 |
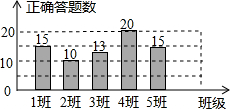 某校举行“汉字听写比赛”,5个班级代表队的正确答题数如图.这5个正确答题数所组成的一组数据的中位数和众数分别是( )
某校举行“汉字听写比赛”,5个班级代表队的正确答题数如图.这5个正确答题数所组成的一组数据的中位数和众数分别是( )| A. | 10,15 | B. | 13,15 | C. | 13,20 | D. | 15,15 |
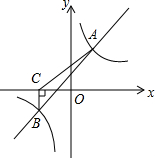 如图所示,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,4),B(-4,n)两点.
如图所示,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,4),B(-4,n)两点.