题目内容
6.当(a-2)(a-3)=0时,求代数式(a-$\frac{a}{a+1}$)÷$\frac{{a}^{2}-2a}{{a}^{2}-4}$×$\frac{1}{a+2}$的值.分析 先算括号内的减法,把除法变成乘法,算乘法,最后代入求出即可.
解答 解:(a-$\frac{a}{a+1}$)÷$\frac{{a}^{2}-2a}{{a}^{2}-4}$×$\frac{1}{a+2}$
=$\frac{a(a+1)-a}{a+1}$•$\frac{(a+2)(a-2)}{a(a-2)}$•$\frac{1}{a+2}$
=$\frac{{a}^{2}}{a+1}$•$\frac{(a+2)(a-2)}{a(a-2)}$•$\frac{1}{a+2}$
=$\frac{a}{a+1}$,
(a-2)(a-3)=0,
a=2或3,
根据分母不能为0,a=2舍去,
当a=3时,原式=$\frac{3}{4}$.
点评 本题考查了分式的混合运算和求值,能正确根据分式的运算法则进行化简是解此题的关键.

练习册系列答案
相关题目
1.观察下表,回答问题:
(1)数字60、x、y是第29行;
(2)结合表格及相关知识,求x、y的值.
| 4 | 3 | 5 | 32+42=52 |
| 6 | 8 | 10 | 62+82=102 |
| 8 | 15 | 17 | 82+152=172 |
| 10 | 24 | 26 | 102+242=262 |
| … | … | … | … |
| 60 | x | y | 602+x2=y2 |
| … | … | … | … |
(2)结合表格及相关知识,求x、y的值.
15.2009年6月大连“樱桃节”组织16辆汽车装运A,B,C三种樱桃共50吨运往外地销售,按计划,16辆汽车都要装运,每辆汽车只能装运同一种樱桃,且必须装满,根据下表提供的信息,解决下列两个问题;
(1)若装运A种樱桃的车辆为m辆,请用含m的式子表示装运B,C两种樱桃的车辆数;
(2)若装运每种樱桃的车辆数都不少于1辆,请你设计车辆的安排方案,并说明理由.
| 樱桃品种 | A | B | C |
| 每辆汽车运载量(吨) | 2 | 4 | 10 |
(2)若装运每种樱桃的车辆数都不少于1辆,请你设计车辆的安排方案,并说明理由.
16.某市政府将对江边一处废弃荒地进行绿化,要求栽植甲、乙两种不同的树苗共6000棵,且甲种树苗不得多于乙种树苗,某承包商以26万元的报价中标承包了这项工程.根据调查及相关资料表明:移栽一棵树苗的平均费用为8元,甲、乙两种树苗的购买价如表:
设购买甲种树苗x棵,承包商获得的利润为y元.请解答下列问题:
(1)求y与x之间的函数关系式;
(2)若栽植这批树苗全部成活,承包商要获得不低于中标价16%的利润,应如何选购树苗?最大利润是多少?
| 品种 | 购买价(元/棵) |
| 甲 | 20 |
| 乙 | 32 |
(1)求y与x之间的函数关系式;
(2)若栽植这批树苗全部成活,承包商要获得不低于中标价16%的利润,应如何选购树苗?最大利润是多少?
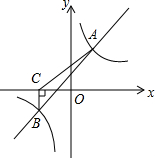 如图所示,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,4),B(-4,n)两点.
如图所示,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,4),B(-4,n)两点.