题目内容
18.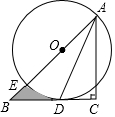 如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.
如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.(1)求证:AD平分∠BAC;
(2)若CD=1,求图中阴影部分的面积(结果保留π).
分析 (1)连接DE,OD.利用弦切角定理,直径所对的圆周角是直角,等角的余角相等证明∠DAO=∠CAD,进而得出结论;
(2)根据等腰三角形的性质得到∠B=∠BAC=45°,由BC相切⊙O于点D,得到∠ODB=90°,求得OD=BD,∠BOD=45°,设BD=x,则OD=OA=x,OB=$\sqrt{2}$x,根据勾股定理得到BD=OD=$\sqrt{2}$,于是得到结论.
解答 (1)证明:连接DE,OD.
∵BC相切⊙O于点D,
∴∠CDA=∠AED,
∵AE为直径,
∴∠ADE=90°,
∵AC⊥BC,
∴∠ACD=90°,
∴∠DAO=∠CAD,
∴AD平分∠BAC;
(2)∵在Rt△ABC中,∠C=90°,AC=BC,
∴∠B=∠BAC=45°,
∵BC相切⊙O于点D,
∴∠ODB=90°,
∴OD=BD,∴∠BOD=45°,
设BD=x,则OD=OA=x,OB=$\sqrt{2}$x,
∴BC=AC=x+1,
∵AC2+BC2=AB2,
∴2(x+1)2=($\sqrt{2}$x+x)2,
∴x=$\sqrt{2}$,
∴BD=OD=$\sqrt{2}$,
∴图中阴影部分的面积=S△BOD-S扇形DOE=$\frac{1}{2}×$$\sqrt{2}×\sqrt{2}$-$\frac{45•π×(\sqrt{2})^{2}}{360}$=1-$\frac{π}{4}$.
点评 本题主要考查了切线的性质,角平分线的定义,扇形面积的计算和勾股定理.熟练掌握切线的性质是解题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
9.某大型商场进了一批成本为8元/件的儿童背心,调查发现,这种背心每周的销售量y(件)与它的定价x(元/件)的关系如下表;(x取整数)
(1)求这种儿童背心每周的销售量y(件)与它的定价x(元/件)之间的函数关系式(不必写出自变量x取值范围);
(2)为使商场每周获得最大利润,试问这种背心定价应为多少?最大利利润是多少?
(3)若商场每周想要获得不低于1050元的利润,试确定这种儿童背心的定价x(元/件)的取值范围.
| x(元/件) | 10 | 12 | 14 | 16 |
| y(件) | 200 | 180 | 160 | 140 |
(2)为使商场每周获得最大利润,试问这种背心定价应为多少?最大利利润是多少?
(3)若商场每周想要获得不低于1050元的利润,试确定这种儿童背心的定价x(元/件)的取值范围.
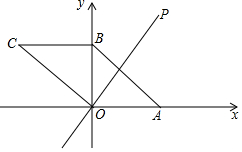 如图,在平面直角坐标系xOy中,?ABCO的顶点A,B的坐标分别是A(3,0),B(0,2).动点P在直线y=$\frac{3}{2}$x上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与?ABCO的边相切时,P点的坐标为(0,0)或($\frac{2}{3}$,1)或(3-$\sqrt{5}$,$\frac{9-3\sqrt{5}}{2}$).
如图,在平面直角坐标系xOy中,?ABCO的顶点A,B的坐标分别是A(3,0),B(0,2).动点P在直线y=$\frac{3}{2}$x上运动,以点P为圆心,PB长为半径的⊙P随点P运动,当⊙P与?ABCO的边相切时,P点的坐标为(0,0)或($\frac{2}{3}$,1)或(3-$\sqrt{5}$,$\frac{9-3\sqrt{5}}{2}$). 如图,港口B在港口A的正东方向,一艘船从港口A出发,沿北偏东75°方向航行20海里到C处,此时测得港口B在C的南偏东45°方向,求C到港口B的距离,(结果保留到0.01海里)(参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,港口B在港口A的正东方向,一艘船从港口A出发,沿北偏东75°方向航行20海里到C处,此时测得港口B在C的南偏东45°方向,求C到港口B的距离,(结果保留到0.01海里)(参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)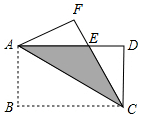 如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.
如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.
 如图所示,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,4),B(-4,n)两点.
如图所示,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,4),B(-4,n)两点.