题目内容
9.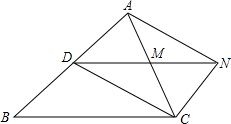 已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.
已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.①求证:AD=CN;
②请添加一个条件,使四边形ADCN是矩形.并证明.
分析 ①根据两直线平行,内错角相等求出∠DAC=∠NCA,然后利用“角边角”证明△AMD和△CMN全等,根据全等三角形对应边相等可得AD=CN;
②先判定四边形ADCN是平行四边形,再根据平行四边形的对边相等即可得证,利用有一个角是直角的平行四边形是矩形直接判断即可.
解答 解:①∵CN∥AB,
∴∠DAC=∠NCA,
在△AMD和△CMN中,
$\left\{\begin{array}{l}{∠DAC=∠NCA}\\{MA=MC}\\{∠AMD=∠CMN}\end{array}\right.$,
∴△AMD≌△CMN(ASA),
∴AD=CN,
②∠BAN=90°,
∵AD∥CN,AD=CN,
∴四边形ADCN是平行四边形,
∵∠BAN=90°,四边形ADCN是平行四边形,
∴四边形ADCN是矩形.
点评 本题考查了矩形的判定,平行四边形的判定与性质,全等三角形的判定与性质,熟练掌握平行四边形与矩形之间的关系,并由第一问求出四边形ADCN是平行四边形是解题的关键.

练习册系列答案
相关题目
20.下列二次根式中,最简二次根式的是( )
| A. | $\sqrt{24}$ | B. | $\sqrt{\frac{b}{a}}$ | C. | $\sqrt{a+4}$ | D. | $\sqrt{50}$ |
14.一个六边形,每一个内角都相等,每个内角的度数为( )
| A. | 100° | B. | 120° | C. | 135° | D. | 150° |
18.下列图形中,由∠1=∠2,能使AB∥CD成立的是( )
| A. |  | B. |  | C. |  | D. |  |
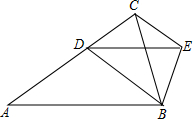 如图,在△ABC中,AB=AC,点D在边AC上,AD=BD=DE,联结BE,∠ABC=∠DBE=72°;
如图,在△ABC中,AB=AC,点D在边AC上,AD=BD=DE,联结BE,∠ABC=∠DBE=72°;