题目内容
15.定义:如果一条直线能够将一个封闭图形的周长和面积平分,那么就把这条直线称作这个封闭图形的等分线.(1)请在如下的三个图形中,分别画出各图形的一条等分线.

(2)请在图中画一条直线l,使它即是矩形的等分线,也是圆的等分线.

(3)如图,在 Rt△ABC中,∠A=90°,AB=3,AC=4,点P是边AB上的动点,问是否存在过点P的等分线?若存在,求出AP的长,若不存在,请说明理由.

分析 (1)圆中过圆心画一条直线,平行四边形中过对称中心画一条直线,等腰三角形中作底边的垂直平分线即可;
(2)过矩形对角线交点和圆心画一条直线即可;
(3)设AP=x,PQ为二分线,则Q在BC边上,BP=3-x,CQ=6-4-x=2-x,BQ=5-(2-x)=x+3,过点Q作QE⊥AB于E,利用相似三角形的性质得出QE=$\frac{4}{5}(x+3)$,再根据S△PBQ=3,得到$\frac{1}{2}$(3-x)•$\frac{4}{5}(x+3)$=3,进而得到x的值.
解答 解:(1)如图所示: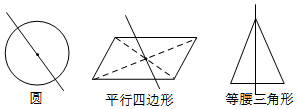
(2)如图所示: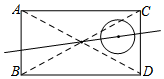
(3)存在过点P的等分线,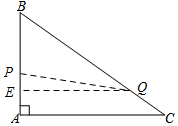
理由:∵Rt△ABC中,∠A=90°,AB=3,AC=4,
∴BC=5,
∴△ABC的周长为12,面积为6,
设AP=x,PQ为二分线,则Q在BC边上,BP=3-x,CQ=6-4-x=2-x,BQ=5-(2-x)=x+3,
过点Q作QE⊥AB于E,则QE=$\frac{4}{5}(x+3)$,
∵S△PBQ=3,
∴$\frac{1}{2}$(3-x)•$\frac{4}{5}(x+3)$=3,
∴x=$\frac{1}{2}\sqrt{6}$.
∴AP=$\frac{1}{2}\sqrt{6}$.
点评 此题属于四边形综合题,主要考查了中心对称图形以及相似三角形的性质等知识的综合应用,根据圆、平行四边形是中心对称图形以及等腰三角形是轴对称图形进行判断是解题关键.

练习册系列答案
相关题目
5.已知二次函数y=ax2+bx+1(a≠0)的图象过点(1,0),且顶点在第二象限,设P=a-b,则P的取值范围是( )
| A. | -1<P<0 | B. | -1<P<1 | C. | 0<P<1 | D. | 1<P<2 |
6.下列各式计算正确的是( )
| A. | -32=-6 | B. | (-3)2=-9 | C. | -32=-9 | D. | -(-3)2=9 |
3.若正比例函数的图象经过点(-1,2),(-m,4-2m),则m的值为( )
| A. | -1 | B. | -2 | C. | 2 | D. | 1 |
10.已知一次函数y=kx+b,经过A(0,3),B(1,2)两点,则它的图象经过( )
| A. | 第一、二、三象限 | B. | 第一、三、四象限 | C. | 第一、二、四象限 | D. | 第二、三、四象限 |
20.下列计算的结果正确的是( )
| A. | (-2a2)•3a=6a3 | B. | (-2x2)3=-8x6 | C. | a3+2a2=2a5 | D. | a3+a3=2a6 |
7. 如图,AD∥BC,AC平分∠BAD,∠1=51°,则∠B的大小为( )
如图,AD∥BC,AC平分∠BAD,∠1=51°,则∠B的大小为( )
 如图,AD∥BC,AC平分∠BAD,∠1=51°,则∠B的大小为( )
如图,AD∥BC,AC平分∠BAD,∠1=51°,则∠B的大小为( )| A. | 51° | B. | 60° | C. | 78° | D. | 88° |
4.下列运算能用平方差公式的是( )
| A. | (a+b)(-a+b) | B. | (m+n)(m+n) | C. | (-2x+y)(2x-y) | D. | -(p-q)(q-p) |