题目内容
3.若正比例函数的图象经过点(-1,2),(-m,4-2m),则m的值为( )| A. | -1 | B. | -2 | C. | 2 | D. | 1 |
分析 根据点的坐标利用待定系数法即可求出正比例函数解析式,再根据一次函数图象上点的坐标特征即可得出关于m的一元一次方程,解之即可得出结论.
解答 解:设正比例函数解析式为y=kx(k≠0),
将(-1,2)代入y=kx中,
2=-k,解得:k=-2.
∴正比例函数解析式为y=-2x.
∵点(-m,4-2m)在正比例函数y=-2x的图象上,
∴4-2m=2m,
解得:m=1.
故选D.
点评 本题考查了待定系数法求一次函数解析式以及一次函数图象上点的坐标特征,根据点的坐标利用待定系数法求出正比例函数解析式是解题的关键.

练习册系列答案
相关题目
13.巡道员沿着一条南北向的铁路进行巡道,他从住地出发,先向南走了4km,休息之后又向南走了3km,然后折返向北走了8.5km,此时,他在所在地的方向,与住地的距离分别是( )
| A. | 南边,-1.5km | B. | 北边、-1.5km | C. | 南边、1.5km | D. | 北边、1.5km |
14.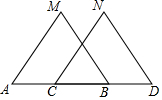 如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
 如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )| A. | ∠M=∠N | B. | AM∥CN | C. | AB=CD | D. | AM=CN |
11.一元二次方程x2-3x=0的根是( )
| A. | x=0或x=-3 | B. | x=3 | C. | x=0 | D. | x=0或x=3 |
18. a,b为有理数,在数轴上的位置如图所示,则下列关于a,b,0三者之间的大小关系,表示正确的是( )
a,b为有理数,在数轴上的位置如图所示,则下列关于a,b,0三者之间的大小关系,表示正确的是( )
 a,b为有理数,在数轴上的位置如图所示,则下列关于a,b,0三者之间的大小关系,表示正确的是( )
a,b为有理数,在数轴上的位置如图所示,则下列关于a,b,0三者之间的大小关系,表示正确的是( )| A. | 0<a<b | B. | b<0<a | C. | b>0>a | D. | a<b<0 |
8.计算(-3a2b3)2的结果是( )
| A. | -9a4b6 | B. | 9a4b6 | C. | 9a4b5 | D. | 6a4b6 |
12.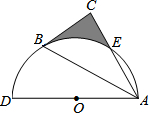 如图,B,E是以AD为直径的半圆O的三等分点,弧BE的长为$\frac{2}{3}$π,∠C=90°,则图中阴影部分的面积为( )
如图,B,E是以AD为直径的半圆O的三等分点,弧BE的长为$\frac{2}{3}$π,∠C=90°,则图中阴影部分的面积为( )
 如图,B,E是以AD为直径的半圆O的三等分点,弧BE的长为$\frac{2}{3}$π,∠C=90°,则图中阴影部分的面积为( )
如图,B,E是以AD为直径的半圆O的三等分点,弧BE的长为$\frac{2}{3}$π,∠C=90°,则图中阴影部分的面积为( )| A. | $\frac{π}{9}$ | B. | $\frac{{\sqrt{3}π}}{9}$ | C. | $\frac{{3\sqrt{3}}}{2}-\frac{2π}{3}$ | D. | $\frac{{3\sqrt{3}}}{2}-\frac{{\sqrt{3}π}}{2}$ |
13. 如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )
如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )
 如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )
如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )| A. | ∠A=∠D | B. | BC=EF | C. | AC=DF | D. | ∠ACB=∠F |


