题目内容
 如图,AB是⊙O的直径,AM和BN是它的两条切线,CD切⊙O于点E,交AM于点D,交BN于点C,F是CD的中点,连接OF.
如图,AB是⊙O的直径,AM和BN是它的两条切线,CD切⊙O于点E,交AM于点D,交BN于点C,F是CD的中点,连接OF.(1)求证:OD∥BE;
(2)猜想:OF与CD有何数量关系?并说明理由;
(3)连接AE、OC分别交OD、BE于G、H,连接GH,若OD=6,OC=8,求GH的长.
考点:圆的综合题
专题:计算题
分析:(1)根据切线长定理由AM、DC是⊙O的切线得DA=DE,OD平分∠ADE,则利用等腰三角形的性质得OD⊥AE,再根据切线的性质由AB为⊙O的直径得到∠AEB=90°,然后根据平行线的性质即可得到OD∥BE;
(2)根据切线的性质得OA⊥AM,OB⊥BN,则AM∥BN,即四边形ABCD为直角梯形,易得OF为梯形ABCD的中位线,根据梯形的中位线性质有OF=
(AD+BC),再根据切线长定理得到CB=CE,DA=DE,所以AD+BC=DE+CE=CD,即可得到=
CD;
(3)连接OE,如图,在(1)中以证明OD垂直平分AE,即点G为AE的中点,同理得到点H为BE的中点,于是得到GH为△AEB的中位线,所以GH=
AB,再判断△DOC为直角三角形,∠COD=90°,根据勾股定理计算出CD=10,利用面积计算出OE=
,则GH=
AB=OE=
.
(2)根据切线的性质得OA⊥AM,OB⊥BN,则AM∥BN,即四边形ABCD为直角梯形,易得OF为梯形ABCD的中位线,根据梯形的中位线性质有OF=
| 1 |
| 2 |
| 1 |
| 2 |
(3)连接OE,如图,在(1)中以证明OD垂直平分AE,即点G为AE的中点,同理得到点H为BE的中点,于是得到GH为△AEB的中位线,所以GH=
| 1 |
| 2 |
| 24 |
| 5 |
| 1 |
| 2 |
| 24 |
| 5 |
解答:(1)证明:∵AM、DC是⊙O的切线,
∴DA=DE,OD平分∠ADE,
∴OD⊥AE,
∵AB为⊙O的直径,
∴∠AEB=90°,
∴BE⊥AE,
∴OD∥BE;
(2)解:OF=
CD.理由如下:
∵AB是⊙O的直径,AM和BN是它的两条切线,
∴OA⊥AM,OB⊥BN,
∴AM∥BN,
∴四边形ABCD为直角梯形,
∵OA=OB,
∴OF为梯形ABCD的中位线,
∴OF=
(AD+BC),
∵BN、CD是⊙O的切线,
∴CB=CE,
∴AD+BC=DE+CE=CD,
∴OF=
CD;
(3)解:连接OE,如图,OD垂直平分AE,
∴点G为AE的中点,
同理得到点H为BE的中点,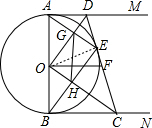
∴GH为△AEB的中位线,
∴GH=
AB,
∵OF=
CD,CF=DF,即OF=DF=CF,
∴△DOC为直角三角形,∠COD=90°,
在Rt△COD中,∵OD=6,OC=8,
∴CD=
=10,
∵CD切⊙O于E,
∴OE⊥CD,
∴
OE•CD=
OC•OD,
∴OE=
=
,
∴AB=2OE=
,
∴GH=
AB=
.
∴DA=DE,OD平分∠ADE,
∴OD⊥AE,
∵AB为⊙O的直径,
∴∠AEB=90°,
∴BE⊥AE,
∴OD∥BE;
(2)解:OF=
| 1 |
| 2 |
∵AB是⊙O的直径,AM和BN是它的两条切线,
∴OA⊥AM,OB⊥BN,
∴AM∥BN,
∴四边形ABCD为直角梯形,
∵OA=OB,
∴OF为梯形ABCD的中位线,
∴OF=
| 1 |
| 2 |
∵BN、CD是⊙O的切线,
∴CB=CE,
∴AD+BC=DE+CE=CD,
∴OF=
| 1 |
| 2 |
(3)解:连接OE,如图,OD垂直平分AE,
∴点G为AE的中点,
同理得到点H为BE的中点,

∴GH为△AEB的中位线,
∴GH=
| 1 |
| 2 |
∵OF=
| 1 |
| 2 |
∴△DOC为直角三角形,∠COD=90°,
在Rt△COD中,∵OD=6,OC=8,
∴CD=
| OD2+OC2 |
∵CD切⊙O于E,
∴OE⊥CD,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴OE=
| 6×8 |
| 10 |
| 24 |
| 5 |
∴AB=2OE=
| 48 |
| 5 |
∴GH=
| 1 |
| 2 |
| 24 |
| 5 |
点评:本题考查了圆的综合题:熟练掌握切线的性质、切线长定理、等腰三角形的性质和三角形与梯形的中位线定理;会运用勾股定理和三角形面积公式进行几何计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
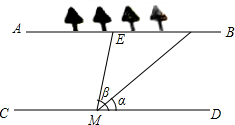 小明所在小组要测量护城河的宽度,如图所示是护城河的一段,AB、CD是两岸(两岸平行),河岸AB上有一排树,相邻两棵树之间的距离均为10米(树粗忽略不计).小明用测角仪在河岸CD的M处观测右数第一、四两棵树,观测线与CD所夹锐角分别为α、β.请你根据这些数据帮小明他们算出河宽(结果用含α、β的式子表示).
小明所在小组要测量护城河的宽度,如图所示是护城河的一段,AB、CD是两岸(两岸平行),河岸AB上有一排树,相邻两棵树之间的距离均为10米(树粗忽略不计).小明用测角仪在河岸CD的M处观测右数第一、四两棵树,观测线与CD所夹锐角分别为α、β.请你根据这些数据帮小明他们算出河宽(结果用含α、β的式子表示).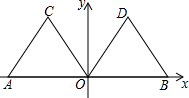 如图,在平面直角坐标系xOy中,点A的坐标为(-2,0),等边三角形AOC经过平移或轴对称都可以得到△OBD.
如图,在平面直角坐标系xOy中,点A的坐标为(-2,0),等边三角形AOC经过平移或轴对称都可以得到△OBD.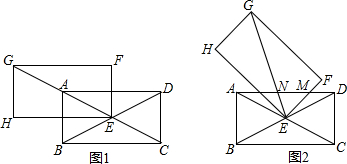
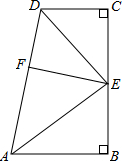 如图,∠B=∠C=90°,E是BC的中点,EF⊥AD于点F,DE平分∠ADC,∠CED=35°,则∠EAB=
如图,∠B=∠C=90°,E是BC的中点,EF⊥AD于点F,DE平分∠ADC,∠CED=35°,则∠EAB=