题目内容
12. 如图,在平面直角坐标系中,直线y=-$\frac{3}{2}x+3$与矩形OABC的边AB、BC分别交于点E、F,若点B的坐标为(m,2),则m的值可能为( )
如图,在平面直角坐标系中,直线y=-$\frac{3}{2}x+3$与矩形OABC的边AB、BC分别交于点E、F,若点B的坐标为(m,2),则m的值可能为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
分析 求出点F和直线y=-$\frac{3}{2}x+3$与x轴交点的坐标,即可判断m的范围,由此可以解决问题.
解答 解:∵B、F两点的纵坐标相同,B点的纵坐标为2,
∴点F的纵坐标为2,
∵点F在y=-$\frac{3}{2}x+3$上,
∴点F的坐标( $\frac{2}{3}$,2),
∵直线y=-$\frac{3}{2}x+3$与x轴的交点为(2,0),
∴由图象可知点B的横坐标 $\frac{2}{3}$<m<2,
∴m=$\frac{3}{2}$.
故选B.
点评 本题考查一次函数图象上的点的坐标特征,解题的关键是知道点的位置能确定点的坐标,是数形结合的好题目,属于中考常考题型.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
2.下列运算中,结果等于a5的是( )
| A. | a2+a3 | B. | a10÷a2 | C. | a3•a2 | D. | (a2)3 |
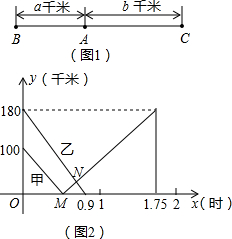 金温高铁于2015年12月26日正式开通,且被誉为“浙江最美高铁”的线路.如图1所示,已知金温高铁上有A,B,C三站,B,C两站相距280千米,甲、乙两列动车分别从B,C两站同时沿铁路匀速相向出发向终点站C,B而行,甲、乙两动车离A站的距离y(千米)与行驶时间x(时)的关系如图2所示,很据图象,解答以下问题:
金温高铁于2015年12月26日正式开通,且被誉为“浙江最美高铁”的线路.如图1所示,已知金温高铁上有A,B,C三站,B,C两站相距280千米,甲、乙两列动车分别从B,C两站同时沿铁路匀速相向出发向终点站C,B而行,甲、乙两动车离A站的距离y(千米)与行驶时间x(时)的关系如图2所示,很据图象,解答以下问题: