题目内容
17.分解因式:x2y-6xy+9y=y(x-3)2.分析 原式提取y,再利用完全平方公式分解即可.
解答 解:原式=y(x2-6x+9)=y(x-3)2,
故答案为:y(x-3)2
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
7.在△ABC中,∠A=90°,AB=3,BC=5,则sinB的值是( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
8.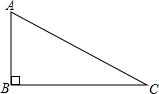 如图,△ABC中,∠B=90°,AB=3,BC=4,则cosA等于( )
如图,△ABC中,∠B=90°,AB=3,BC=4,则cosA等于( )
 如图,△ABC中,∠B=90°,AB=3,BC=4,则cosA等于( )
如图,△ABC中,∠B=90°,AB=3,BC=4,则cosA等于( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
12. 如图,在平面直角坐标系中,直线y=-$\frac{3}{2}x+3$与矩形OABC的边AB、BC分别交于点E、F,若点B的坐标为(m,2),则m的值可能为( )
如图,在平面直角坐标系中,直线y=-$\frac{3}{2}x+3$与矩形OABC的边AB、BC分别交于点E、F,若点B的坐标为(m,2),则m的值可能为( )
 如图,在平面直角坐标系中,直线y=-$\frac{3}{2}x+3$与矩形OABC的边AB、BC分别交于点E、F,若点B的坐标为(m,2),则m的值可能为( )
如图,在平面直角坐标系中,直线y=-$\frac{3}{2}x+3$与矩形OABC的边AB、BC分别交于点E、F,若点B的坐标为(m,2),则m的值可能为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
9.下列运算中,正确的是( )
| A. | x•x3=x3 | B. | (x2)3=x5 | C. | x6÷x2=x4 | D. | (x-y)2=x2+y2 |
6.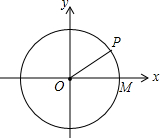 在平面直角坐标系中,以原点O为圆心的⊙O交x轴正半轴为M,P为圆上一点,坐标为($\sqrt{3}$,1),则cos∠POM=( )
在平面直角坐标系中,以原点O为圆心的⊙O交x轴正半轴为M,P为圆上一点,坐标为($\sqrt{3}$,1),则cos∠POM=( )
 在平面直角坐标系中,以原点O为圆心的⊙O交x轴正半轴为M,P为圆上一点,坐标为($\sqrt{3}$,1),则cos∠POM=( )
在平面直角坐标系中,以原点O为圆心的⊙O交x轴正半轴为M,P为圆上一点,坐标为($\sqrt{3}$,1),则cos∠POM=( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
7.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (3a)3=9a3 | C. | a3-2a3=-1 | D. | (a2)3=a6 |
 甲、乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA(l货)表示货车离甲地距离y(千米)与货车出发时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与货车出发时间x(小时)之间的函数关系,请根据图象解答下列问题:
甲、乙两地相距400千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA(l货)表示货车离甲地距离y(千米)与货车出发时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与货车出发时间x(小时)之间的函数关系,请根据图象解答下列问题: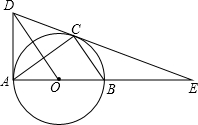 如图,△ABC内接于⊙O,AB为直径,E为AB延长线上的点,作OD∥BC交EC的延长线于点D,连接AD.
如图,△ABC内接于⊙O,AB为直径,E为AB延长线上的点,作OD∥BC交EC的延长线于点D,连接AD.