题目内容
3.甲、乙两同学分别解同一个二次系数为1的一元二次方程,甲因把一次项系数看错了,而解得方程的两根为-2和3,乙把常数看错了,解得两根为1+$\sqrt{3}$和1-$\sqrt{3}$,则原方程是x2-2x-6=0.分析 先设这个方程的两根是α、β,由于甲把一次项系数看错了,而解得方程的两根为-2和3,则有αβ=$\frac{c}{a}$=-6,乙把常数项看错了,解得两根为1+$\sqrt{3}$和1-$\sqrt{3}$,则有α+β=-$\frac{b}{a}$=2,令a=1,那么关于α、β的一元二次方程可求.
解答 解:设此方程的两个根是α、β,根据题意得
α+β=-$\frac{b}{a}$=2,αβ=$\frac{c}{a}$=-6,
令a=1,那么关于α、β的一元二次方程是x2-2x-6=0.
故答案为x2-2x-6=0.
点评 此题主要考查了根与系数的关系,若x1、x2是方程ax2+bx+c=0的两根,则有x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.下列运算正确的是( )
| A. | a4+a5=a9 | B. | 2a4×3a5=6a9 | C. | (a3)2÷a5=a10 | D. | (-a3)4=a7 |
8.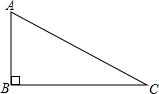 如图,△ABC中,∠B=90°,AB=3,BC=4,则cosA等于( )
如图,△ABC中,∠B=90°,AB=3,BC=4,则cosA等于( )
 如图,△ABC中,∠B=90°,AB=3,BC=4,则cosA等于( )
如图,△ABC中,∠B=90°,AB=3,BC=4,则cosA等于( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
12. 如图,在平面直角坐标系中,直线y=-$\frac{3}{2}x+3$与矩形OABC的边AB、BC分别交于点E、F,若点B的坐标为(m,2),则m的值可能为( )
如图,在平面直角坐标系中,直线y=-$\frac{3}{2}x+3$与矩形OABC的边AB、BC分别交于点E、F,若点B的坐标为(m,2),则m的值可能为( )
 如图,在平面直角坐标系中,直线y=-$\frac{3}{2}x+3$与矩形OABC的边AB、BC分别交于点E、F,若点B的坐标为(m,2),则m的值可能为( )
如图,在平面直角坐标系中,直线y=-$\frac{3}{2}x+3$与矩形OABC的边AB、BC分别交于点E、F,若点B的坐标为(m,2),则m的值可能为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
13.下列运算正确的是( )
| A. | (2a2)3=6a6 | B. | -x6÷x2=-x4 | C. | 2x+2y=4xy | D. | (x-1)2=x2-12 |
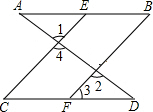 如图,已知AD与AB、CD交于A、D两点,EC、BF与AB、CD交于E、C、B、F,且∠1=∠2,∠B=∠C.
如图,已知AD与AB、CD交于A、D两点,EC、BF与AB、CD交于E、C、B、F,且∠1=∠2,∠B=∠C.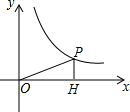 如图,P(12,a)在反比例函数$y=\frac{60}{x}$图象上,PH⊥x轴于H,则tan∠POH的值为$\frac{5}{12}$.
如图,P(12,a)在反比例函数$y=\frac{60}{x}$图象上,PH⊥x轴于H,则tan∠POH的值为$\frac{5}{12}$.