题目内容
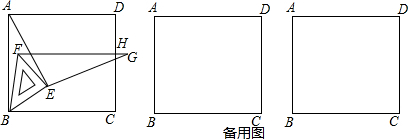
11.如图,将等腰直角三角板放在正方形ABCD的顶点B处,且三角板中BE=EF.连AE,再作EG⊥AE且EG=AE.绕点B旋转三角板,并保证线段FG与正方形的边CD交于点H.(1)求证:△ABE≌△GFE.
(2)当DH取得最小值时,求∠ABE的度数.
(3)当三角板有两个顶点在边BC上时,求$\frac{GH}{EF}$的值.
分析 (1)由等腰直角三角板和正方形ABCD的特点,直接得到△ABE≌△GFE.
(2)由△ABE≌△GFE得到的条件判断出MH⊥AB,再判断DH最小时的位置,即可;
(3)由△APE≌△ECG得到结论,判断出△HCG是等腰直角三角形,即可求出结果.
解答 解:(1)证明:在△ABE和△GFE中,
$\left\{\begin{array}{l}{BE=FE}\\{∠AEB=∠CEF}\\{AE=CE}\end{array}\right.$,
∴△ABE≌△GFE,
(2)如图,∵△ABE≌△GFE,
∴∠BAE=∠FGE,
∵∠AMN=∠EMG,
∴∠ANM=∠MEG=90°,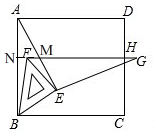 ∴MH⊥AB,
∴MH⊥AB,
∴四边形ANHG是矩形,
∴DH=AN,
要使DH最小,则BN最大,
∵BN≤BF,
∴当BF与BN重合时,AN最小,
∴∠ABE=∠FBE=45°
(3)如图1,
由(1)知,∴△ABE≌△GFE,
∴AB=FG,∠ABE=∠GFE,
∴BC=FG,FG∥BC,
∴四边形CEFG是平行四边形,
∴∠ECG=∠BFG=135°,
∴△HCG是等腰直角三角形,
∴HG=CH=FE,
∴$\frac{HG}{EF}=1$,
∵FG=AB=BC,
∴HG=BF,
∴$\frac{GH}{EF}=\sqrt{2}$.
点评 此题是几何变换综合题,主要考查了全等三角形的性质和判定,等腰直角三角形判定和性质,即二倍体的关键是判断三角形全等.

练习册系列答案
相关题目
1.如果把分式$\frac{x-y}{x+y}$中的x和y都扩大了3倍,那么分式的值( )
| A. | 扩大3倍 | B. | 不变 | C. | 缩小3倍 | D. | 缩小6倍 |
2.下列图形中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.某小组5名同学在一周内参加家务劳动的时间如下表所示,关于“劳动时间”的这组数据,
以下说法正确的是( )
| 劳动时间(小时) | 3 | 4 | 5 | 6 |
| 人数 | 1 | 1 | 2 | 1 |
| A. | 中位数是5,平均数是3.6 | B. | 众数是5,平均数是4.6 | ||
| C. | 中位数是4,平均数是3.6 | D. | 众数是2,平均数是4.6 |
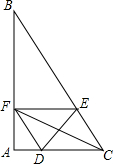 如图,在△ABC中,∠A=90°,∠B=30°,AC=6cm,点D从点A开始以1cm/s的速度向点C运动,点E从点C开始以2cm/s的速度向点B运动,两点同时运动,同时停止,运动的时间为ts,过点E作EF∥AC交AB于点F.
如图,在△ABC中,∠A=90°,∠B=30°,AC=6cm,点D从点A开始以1cm/s的速度向点C运动,点E从点C开始以2cm/s的速度向点B运动,两点同时运动,同时停止,运动的时间为ts,过点E作EF∥AC交AB于点F.