题目内容
17.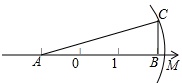 如图,△ABC中,∠ABC=90°,AB=3,BC=1,且AB在数轴上,若以点A(-1,0)为圆心,边AC的长为半径作弧交数轴的正半轴于点M,则点M的坐标为( )
如图,△ABC中,∠ABC=90°,AB=3,BC=1,且AB在数轴上,若以点A(-1,0)为圆心,边AC的长为半径作弧交数轴的正半轴于点M,则点M的坐标为( )| A. | ($\sqrt{5}$-1,0) | B. | (2,0) | C. | ($\sqrt{10}$-1,0) | D. | ($\sqrt{10}$,0) |
分析 在Rt△ABC中利用勾股定理求出AC,继而得出AM的长,结合数轴的知识可得出点M的坐标.
解答 解:由题意得,AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{10}$,
∴AM=$\sqrt{10}$,
∵A(-1,0),
∴OA=1,∴OM=$\sqrt{10}$-1,
∴点M的坐标为($\sqrt{10}$-1,0).
故选C.
点评 此题考查了勾股定理及坐标轴的知识,属于基础题,利用勾股定理求出AC的长度是解答本题的关键,难度一般.

练习册系列答案
相关题目
6.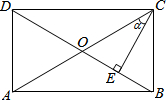 如图,在矩形ABCD中,CE⊥BD于点E,BE=2,DE:BD=4:5,设∠ACE=α,则tanα的值为( )
如图,在矩形ABCD中,CE⊥BD于点E,BE=2,DE:BD=4:5,设∠ACE=α,则tanα的值为( )
 如图,在矩形ABCD中,CE⊥BD于点E,BE=2,DE:BD=4:5,设∠ACE=α,则tanα的值为( )
如图,在矩形ABCD中,CE⊥BD于点E,BE=2,DE:BD=4:5,设∠ACE=α,则tanα的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | 2 |
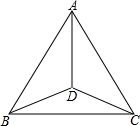 如图,点D是△ABC内部一点,AD平分∠BAC.
如图,点D是△ABC内部一点,AD平分∠BAC.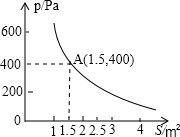 某校技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强是木板面积的反比例函数,其图象如图所示
某校技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强是木板面积的反比例函数,其图象如图所示