题目内容
9.已知一次函数的图象经过A(-2,-3),B(1,3)两点,求这个函数的表达式,并判断P(-1,1)是否在这个函数的图象上.分析 用待定系数法求解函数解析式,将点P坐标代入即可判断.
解答 解:设一次函数的表达式为y=kx+b,
一次函数的图象经过A(-2,-3),B(1,3)两点,
则$\left\{\begin{array}{l}{-2k+b=-3}\\{k+b=3}\end{array}\right.$,解得:k=2,b=1.
∴函数的解析式为:y=2x+1.
将点P(-1,1)代入函数解析式,1≠-2+1,
∴点P不在这个一次函数的图象上.
点评 本题考查了待定系数法求一次函数解析式及一次函数图象上点的坐标特征,难度不大,属于基础题.

练习册系列答案
相关题目
1.把多项式a2+7a-18因式分解的结果是( )
| A. | (a-2)(a+9) | B. | (a-9)(a+2) | C. | (a+6)(a-3) | D. | (a+3)(a-6) |
1.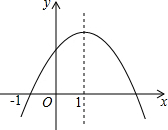 二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:
①2a+b<0;②4a-2b+c=0;③3a+c=0;④a:b:c=-1:2:3.
其中正确的是( )
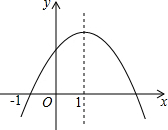 二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:①2a+b<0;②4a-2b+c=0;③3a+c=0;④a:b:c=-1:2:3.
其中正确的是( )
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
17.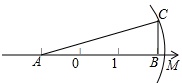 如图,△ABC中,∠ABC=90°,AB=3,BC=1,且AB在数轴上,若以点A(-1,0)为圆心,边AC的长为半径作弧交数轴的正半轴于点M,则点M的坐标为( )
如图,△ABC中,∠ABC=90°,AB=3,BC=1,且AB在数轴上,若以点A(-1,0)为圆心,边AC的长为半径作弧交数轴的正半轴于点M,则点M的坐标为( )
 如图,△ABC中,∠ABC=90°,AB=3,BC=1,且AB在数轴上,若以点A(-1,0)为圆心,边AC的长为半径作弧交数轴的正半轴于点M,则点M的坐标为( )
如图,△ABC中,∠ABC=90°,AB=3,BC=1,且AB在数轴上,若以点A(-1,0)为圆心,边AC的长为半径作弧交数轴的正半轴于点M,则点M的坐标为( )| A. | ($\sqrt{5}$-1,0) | B. | (2,0) | C. | ($\sqrt{10}$-1,0) | D. | ($\sqrt{10}$,0) |