题目内容
5．若$\frac{\sqrt{1-x}}{\sqrt{x+2}}$=$\sqrt{\frac{1-x}{x+2}}$成立，则x的取值范围是-2＜x≤1．分析 直接利用二次根式的性质得出1-x≥0，x+2＞0，求出即可．
解答 解：∵$\frac{\sqrt{1-x}}{\sqrt{x+2}}$=$\sqrt{\frac{1-x}{x+2}}$成立，
∴1-x≥0，x+2＞0，
解得：-2＜x≤1．
故答案为：-2＜x≤1．
点评 此题主要考查了二次根式的性质以及解不等式，正确解不等式是解题关键．
练习册系列答案
经典密卷系列答案
金牌课堂练系列答案
三新快车金牌周周练系列答案
相关题目
如图：在△ABC中，∠B=90°，∠BAC=2∠C，BC=6，AD平分∠BAC，则D到AC的距离为（ ）
17．
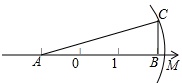如图，△ABC中，∠ABC=90°，AB=3，BC=1，且AB在数轴上，若以点A（-1，0）为圆心，边AC的长为半径作弧交数轴的正半轴于点M，则点M的坐标为（ ）
如图，△ABC中，∠ABC=90°，AB=3，BC=1，且AB在数轴上，若以点A（-1，0）为圆心，边AC的长为半径作弧交数轴的正半轴于点M，则点M的坐标为（ ）| A． | （$\sqrt{5}$-1，0） | B． | （2，0） | C． | （$\sqrt{10}$-1，0） | D． | （$\sqrt{10}$，0） |
如图，AB是⊙O的直径，C是半圆上的一个三等分点，D是$\widehat{AC}$的中点，P是直径AB上一点，⊙O是半径为1，则PC+PD的最小值是$\sqrt{2}$．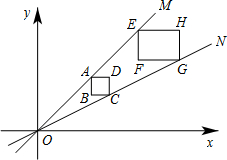
正方形ABCD，矩形EFGH均位于第一象限内，它们的边平行于x轴或y轴，其中，点A，E在直线OM上，点C，G在直线ON上，O为坐标原点，点A的坐标为（3，3），正方形ABCD的边长为1．若矩形EFGH的周长为10，面积为6，则点F的坐标为（7，5），（8，5）．