题目内容
12.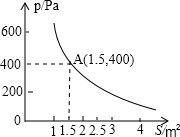 某校技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强是木板面积的反比例函数,其图象如图所示
某校技小组进行野外考察,途中遇到一片十几米宽的烂泥湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺了若干块木块,构筑成一条临时近道.木板对地面的压强是木板面积的反比例函数,其图象如图所示(1)请直接写出这一函数表达式和自变量取值范围;
(2)当木板面积为3m2时,压强是多少?
(3)如果要求压强不超过100pa,木板的面积至少要多大?
分析 (1)由图可知1.5×400=600为定值,即k=600,易求出解析式.
(2)将S=3代入(1)中所求解析式,计算即可求出函数值p.
(3)压强不超过100Pa,即p≤100时,求相对应的自变量的范围.
解答 解:(1)设p=$\frac{k}{S}$.
把A(1.5,400)代入,得400=$\frac{k}{1.5}$,
k=1.5×400=600,
∴p=$\frac{600}{S}$(S>0).
(2)当S=3时,p=$\frac{600}{3}$=200,即压强是200Pa.
(3)由题意知$\frac{600}{S}$≤100,
解得S≥6,
即木板面积至少要有6m2.
点评 此题主要考查反比例函数在实际生活中的应用,解题的关键是从实际问题中整理出函数模型,用反比例函数的知识解决实际问题,同学们要认真观察图象得出正确的结果.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.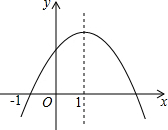 二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:
①2a+b<0;②4a-2b+c=0;③3a+c=0;④a:b:c=-1:2:3.
其中正确的是( )
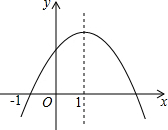 二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:①2a+b<0;②4a-2b+c=0;③3a+c=0;④a:b:c=-1:2:3.
其中正确的是( )
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
17.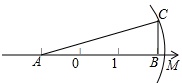 如图,△ABC中,∠ABC=90°,AB=3,BC=1,且AB在数轴上,若以点A(-1,0)为圆心,边AC的长为半径作弧交数轴的正半轴于点M,则点M的坐标为( )
如图,△ABC中,∠ABC=90°,AB=3,BC=1,且AB在数轴上,若以点A(-1,0)为圆心,边AC的长为半径作弧交数轴的正半轴于点M,则点M的坐标为( )
 如图,△ABC中,∠ABC=90°,AB=3,BC=1,且AB在数轴上,若以点A(-1,0)为圆心,边AC的长为半径作弧交数轴的正半轴于点M,则点M的坐标为( )
如图,△ABC中,∠ABC=90°,AB=3,BC=1,且AB在数轴上,若以点A(-1,0)为圆心,边AC的长为半径作弧交数轴的正半轴于点M,则点M的坐标为( )| A. | ($\sqrt{5}$-1,0) | B. | (2,0) | C. | ($\sqrt{10}$-1,0) | D. | ($\sqrt{10}$,0) |
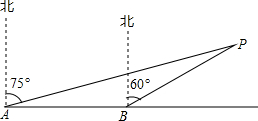 某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,又继续航行18海里后,在B处测得小岛P的方位是北偏东60°.
某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,又继续航行18海里后,在B处测得小岛P的方位是北偏东60°.  画出将三角形ABC绕点O顺时针方向旋转90度后的对应三角形.(保留作图痕迹)
画出将三角形ABC绕点O顺时针方向旋转90度后的对应三角形.(保留作图痕迹)