题目内容
6.为了研究平行四边形的特征,王明、李飞等几个同学对一个平行四边形进行了测量,其结果是:①∠A=50°,∠B=50°,∠C=130°,∠D=130°; ②AB=5,BC=10,CD=5,AD=9;
③∠A=52°,∠B=128°,∠C=50°; ④AB=CD=5,BC=AD=10.
其中不可能发生的是②③.
分析 由平行四边形的对角相等,邻角互补得出①正确,③不正确;由平行四边形的对边相等,得出②不正确,④正确;即可得出结论.
解答 解:∵平行四边形的对角相等,
∠A=∠B=50°,∠C=∠D=130°,∠A+∠B+∠C+∠D═360°,
∴①正确;
∵平行四边形的对边相等,
但AB≠CD,BC≠AD,
∴②不可能发生;
∵平行四边形的对角相等,邻角互补,
但∠A≠∠C,
∴③不可能发生;
∵平行四边形的对边相等,
AB=CD=5,BC=AD=10,
∴④正确;
不可能发生的是②③;
故答案为:②③.
点评 本题考查了平行四边形的性质;熟练掌握平行四边形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
17.轮船在顺水航行90千米比逆水航行90千米少花了3小时,已知水流速度是2千米/时,求轮船在静水中的速度.设轮船在静水中的速度为x千米/时,依据题意列方程得( )
| A. | $\frac{90}{x+2}$+3=$\frac{90}{x-2}$ | B. | $\frac{90}{x-2}$+3=$\frac{90}{x+2}$ | C. | $\frac{90}{x+3}$+2=$\frac{90}{x-3}$ | D. | $\frac{90}{x+3}$-2=$\frac{90}{x-3}$ |
1.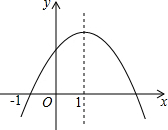 二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:
①2a+b<0;②4a-2b+c=0;③3a+c=0;④a:b:c=-1:2:3.
其中正确的是( )
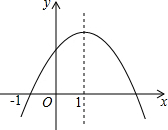 二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:①2a+b<0;②4a-2b+c=0;③3a+c=0;④a:b:c=-1:2:3.
其中正确的是( )
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
17.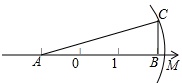 如图,△ABC中,∠ABC=90°,AB=3,BC=1,且AB在数轴上,若以点A(-1,0)为圆心,边AC的长为半径作弧交数轴的正半轴于点M,则点M的坐标为( )
如图,△ABC中,∠ABC=90°,AB=3,BC=1,且AB在数轴上,若以点A(-1,0)为圆心,边AC的长为半径作弧交数轴的正半轴于点M,则点M的坐标为( )
 如图,△ABC中,∠ABC=90°,AB=3,BC=1,且AB在数轴上,若以点A(-1,0)为圆心,边AC的长为半径作弧交数轴的正半轴于点M,则点M的坐标为( )
如图,△ABC中,∠ABC=90°,AB=3,BC=1,且AB在数轴上,若以点A(-1,0)为圆心,边AC的长为半径作弧交数轴的正半轴于点M,则点M的坐标为( )| A. | ($\sqrt{5}$-1,0) | B. | (2,0) | C. | ($\sqrt{10}$-1,0) | D. | ($\sqrt{10}$,0) |
 如图:在△ABC中,∠B=90°,∠BAC=2∠C,BC=6,AD平分∠BAC,则D到AC的距离为( )
如图:在△ABC中,∠B=90°,∠BAC=2∠C,BC=6,AD平分∠BAC,则D到AC的距离为( ) 证明:两组对角分别相等的四边形是平行四边形.
证明:两组对角分别相等的四边形是平行四边形. 如图,AB是⊙O的直径,C是半圆上的一个三等分点,D是$\widehat{AC}$的中点,P是直径AB上一点,⊙O是半径为1,则PC+PD的最小值是$\sqrt{2}$.
如图,AB是⊙O的直径,C是半圆上的一个三等分点,D是$\widehat{AC}$的中点,P是直径AB上一点,⊙O是半径为1,则PC+PD的最小值是$\sqrt{2}$.