题目内容
6. 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1,出租车离甲地的距离为y2,客车行驶时间为x,若y1,y2与x的函数关系图象如图所示,下列四种说法:
一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1,出租车离甲地的距离为y2,客车行驶时间为x,若y1,y2与x的函数关系图象如图所示,下列四种说法:(1)y2关于x的函数关系式为y2=60x(x≥0).
(2)行驶3.75小时,两车相遇.
(3)出租车到达甲地时,两车相距最远.
(4)出租车的速度是客车速度的1.5倍.
其中一定正确的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 (1)令x=0求出y2值,这与图象不符,由此可得出(1)不正确;(2)根据“速度=两地间距离÷行使时间”即可得出客车和出租车的速度,再由“相遇时间=两地距离÷两车速度和”由此即可得出(2)正确;(3)观察函数图象即可得出当x=0时,两车距离最远,即(3)不正确;(4)结合(2)结论即可得出出租车与客车间速度的关系,由此得出(4)不正确.综上即可得出结论.
解答 解:(1)当x=0时,y2=60×0=0,与图象不符,(1)不正确;
(2)出租车的速度为:600÷6=100(km/h);
客车的速度为:600÷10=60(km/h).
两车相遇的时间为:600÷(100+60)=$\frac{15}{4}$=3.75(h),
∴(2)正确;
(3)由函数图象可知:当x=0时,两车距离最远,
∴(3)不正确;
(4)由(2)可知:出租车的速度是客车速度的100÷60=$\frac{5}{3}$,
∵$\frac{5}{3}$≠1.5,
∴(4)不正确.
综上可知正确的结论只有一个.
故选A.
点评 本题考查了一次函数的应用,解题的关键是逐条分析4条结论,验证其是否正确.本题属于基础题,难度不大,解决该题型题目时,结合函数图象,利用数形结合解决问题是关键.

练习册系列答案
相关题目
11. 如图,是雷达探测器测得的结果,图中显示在点A,B,C,D,E,F处有目标出现,目标的表示方法为(r,α),其中,r表示目标与探测器的距离;α表示以正东为始边,逆时针旋转后的角度.例如,点A,D的位置表示为A(5,30°),D(4,240°).用这种方法表示点B,C,E,F的位置,其中正确的是( )
如图,是雷达探测器测得的结果,图中显示在点A,B,C,D,E,F处有目标出现,目标的表示方法为(r,α),其中,r表示目标与探测器的距离;α表示以正东为始边,逆时针旋转后的角度.例如,点A,D的位置表示为A(5,30°),D(4,240°).用这种方法表示点B,C,E,F的位置,其中正确的是( )
 如图,是雷达探测器测得的结果,图中显示在点A,B,C,D,E,F处有目标出现,目标的表示方法为(r,α),其中,r表示目标与探测器的距离;α表示以正东为始边,逆时针旋转后的角度.例如,点A,D的位置表示为A(5,30°),D(4,240°).用这种方法表示点B,C,E,F的位置,其中正确的是( )
如图,是雷达探测器测得的结果,图中显示在点A,B,C,D,E,F处有目标出现,目标的表示方法为(r,α),其中,r表示目标与探测器的距离;α表示以正东为始边,逆时针旋转后的角度.例如,点A,D的位置表示为A(5,30°),D(4,240°).用这种方法表示点B,C,E,F的位置,其中正确的是( )| A. | B(2,90°) | B. | C(2,120°) | C. | E(3,120°) | D. | F(4,210°) |
16. 如图,已知AB=2AD,AC=2AE,则下列结论错误的是( )
如图,已知AB=2AD,AC=2AE,则下列结论错误的是( )
 如图,已知AB=2AD,AC=2AE,则下列结论错误的是( )
如图,已知AB=2AD,AC=2AE,则下列结论错误的是( )| A. | △ABD∽△ACE | B. | ∠B=∠C | C. | BD=2CE | D. | AB•EC=AC•BD |

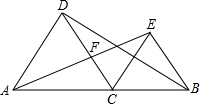 如图,点C是线段AB上一点,△ACD和△BCE都是等边三角形,连结AE,BD,设AE交CD于点F.
如图,点C是线段AB上一点,△ACD和△BCE都是等边三角形,连结AE,BD,设AE交CD于点F.