题目内容
8.画出函数y1=2x-4与y2=-2x+8的图象,观察图象并回答问题:(1)x取何值时,2x-4>0?
(2)x取何值时,-2x+8>0?
(3)x取何值时,2x-4>0与-2x+8>0同时成立?
(4)你能求出函数y1=2x-4与y2=-2x+8的图象与X轴所围成的三角形的面积吗?
分析 利用描点法画出两个一次函数图象,然后利用图象可解决(1)、(2)、(3);利用图象写出两函数图象的交点坐标,然后根据三角形面积公式计算函数y1=2x-4与y2=-2x+8的图象与X轴所围成的三角形的面积.
解答 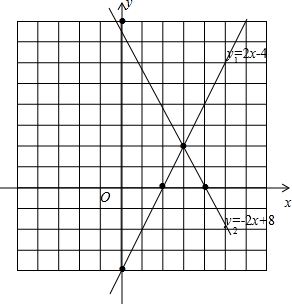 解:如图所示:
解:如图所示:
(1)当x>2时,2x-4>0;
(2)当x=4时,-2x+8=0;
(3)当2<x<4时,2x-4>0与-2x+8>0同时成立;
(4)函数y1=2x-4与y2=-2x+8的图象的交点坐标为(3,2),
所以函数y1=2x-4与y2=-2x+8的图象与X轴所围成的三角形的面积=$\frac{1}{2}$×(4-2)×2=2.
点评 本题考查了一次函数与一元一次不等式:一次函数与一元一次不等式的关系从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.解决本题的关键是准确画出两函数图象.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
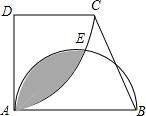 如图,∠D=∠DAB=90°,AD=CD=$\sqrt{3}$,AB=2,以D为圆心,AD为半径作扇形AEC,以AB为直径作半圆,则圆中阴影部分的面积为$\frac{5π}{6}-\sqrt{3}$.
如图,∠D=∠DAB=90°,AD=CD=$\sqrt{3}$,AB=2,以D为圆心,AD为半径作扇形AEC,以AB为直径作半圆,则圆中阴影部分的面积为$\frac{5π}{6}-\sqrt{3}$.