题目内容
16.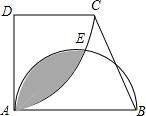 如图,∠D=∠DAB=90°,AD=CD=$\sqrt{3}$,AB=2,以D为圆心,AD为半径作扇形AEC,以AB为直径作半圆,则圆中阴影部分的面积为$\frac{5π}{6}-\sqrt{3}$.
如图,∠D=∠DAB=90°,AD=CD=$\sqrt{3}$,AB=2,以D为圆心,AD为半径作扇形AEC,以AB为直径作半圆,则圆中阴影部分的面积为$\frac{5π}{6}-\sqrt{3}$.
分析 证得△DAO≌△DEO,得到∠ADO=∠EDO,∠DAO=∠DEO=90°,于是求得AD=$\sqrt{3}$,∠ADO=∠EDO=30°,∠AOD=∠EOD=60°,∠ADE=60°,得到∠AOE=120°,由DA=DE,OA=OE,得到AE⊥DO,∠FAO=30°,OF=$\frac{1}{2}$OA=$\frac{1}{2}$,AE=$\sqrt{3}$,由于阴影部分的面积=(S扇形DAE-S△DAE)+(S扇形OAE-S△OAE),把数值代入即可.
解答 解: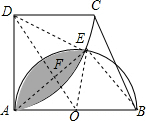 在△DAO和△DEO中,
在△DAO和△DEO中,
$\left\{\begin{array}{l}{DA=DW}\\{OA=OE}\\{DO=DO}\end{array}\right.$,
∴△DAO≌△DEO,
∴∠ADO=∠EDO,∠DAO=∠DEO=90°,
∵OA=$\frac{1}{2}$AB=1,AD=$\sqrt{3}$,
∴∠ADO=∠EDO=30°,
∴∠AOD=∠EOD=60°,∠ADE=60°,
∴∠AOE=120°,
∵DA=DE,OA=OE,∴AE⊥DO,
∴∠FAO=30°,
∴OF=$\frac{1}{2}$OA=$\frac{1}{2}$,AE=$\sqrt{3}$,
∴阴影部分的面积=(S扇形DAE-S△DAE)+(S扇形OAE-S△OAE)=[$\frac{60π•(\sqrt{3})^{2}}{360}$-$\frac{\sqrt{3}}{4}•(\sqrt{3})^{2}$]+[$\frac{120π•{1}^{2}}{360}$-$\frac{1}{2}•\sqrt{3}•\frac{1}{2}$]=$\frac{5π}{6}-\sqrt{3}$,
故答案为$\frac{5π}{6}-\sqrt{3}$.
点评 本题主要考查了全等三角形的判定与性质,圆的切线的性质与判定,含30°的直角三角形的性质,扇形的面积计算,解题的关键是正确作出辅助线利用割补法把不规则图形化为规则图形.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案| A. | x≠1且x≠2 | B. | x≠1或x≠2 | C. | x=1且x=2 | D. | x=1或x=2 |
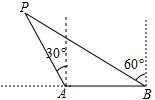 如图,海上有一小岛P,在他周围7海里内有暗礁,一艘轮船以15海里/时的速度由东向西方向航行至B点处测得小岛P在它北偏西60°的方向上,继续向西航行40分钟到达A处,又测得小岛P在它的北偏西30°方向上,如果货轮不改变方向能否继续航行?
如图,海上有一小岛P,在他周围7海里内有暗礁,一艘轮船以15海里/时的速度由东向西方向航行至B点处测得小岛P在它北偏西60°的方向上,继续向西航行40分钟到达A处,又测得小岛P在它的北偏西30°方向上,如果货轮不改变方向能否继续航行?