题目内容
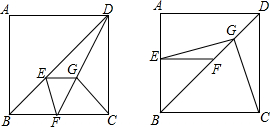
如图,三角形ABC中任意一点P(x0,y0)经平移后对应点为P1 (x0+5,y0+3),将三角形作同样的平移得到三角形A1B1C1,求A1,B1,C1的坐标并求出平移后的三角形A1B1C1的面积.


考点:作图-平移变换
专题:作图题
分析:根据网格结构找出点A、B、C平移后的对应点的A1,B1,C1的位置,然后顺次连接即可;再根据平面直角坐标系写出各点的坐标,利用△A1B1C1的面积等于所在的矩形的面积减去四周三个小直角三角形的面积列式计算即可得解.
解答: 解:△A1B1C1如图所示:
解:△A1B1C1如图所示:
A1(3,6),B1(1,2),C1(7,3);
△A1B1C1的面积=6×4-
×2×4-
×1×6-
×3×4
=24-4-3-6
=24-13
=11.
 解:△A1B1C1如图所示:
解:△A1B1C1如图所示:A1(3,6),B1(1,2),C1(7,3);
△A1B1C1的面积=6×4-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=24-4-3-6
=24-13
=11.
点评:本题考查了利用平移变换作图,三角形的面积,熟练掌握网格结构准确找出对应点的位置是解题的关键.

练习册系列答案
相关题目
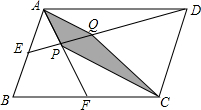 如图,E、F分别是平行四边形ABCD的边AB、BC的中点,DE与AF交于点P,点Q在线段DE上,且AQ∥PC,求梯形APCQ的面积与平行四边形ABCD的面积的比值.
如图,E、F分别是平行四边形ABCD的边AB、BC的中点,DE与AF交于点P,点Q在线段DE上,且AQ∥PC,求梯形APCQ的面积与平行四边形ABCD的面积的比值.